从1,2,…,9中任取n个数,其中一定可以找到若干个数(至少一个,也可以是全部),它们的和能被10整除,求n的最小值.
从1,2,…,9中任取n个数,其中一定可以找到若干个数(至少一个,也可以是全部),它们的和能被10整除,求n的最小值.
发布时间:2025-06-28 07:57:51
从1,2,…,9中任取n个数,其中一定可以找到若干个数(至少一个,也可以是全部),它们的和能被10整除,求n的最小值.
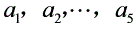 是1,2,…,9中的5个不同的数.若其中任意若干个数,它们的和都不能被10整除,则
是1,2,…,9中的5个不同的数.若其中任意若干个数,它们的和都不能被10整除,则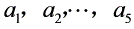 中不可能同时出现1和9;2和8;3和7;4和6.于是
中不可能同时出现1和9;2和8;3和7;4和6.于是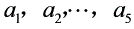 中必定有一个数是5.若
中必定有一个数是5.若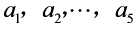 中含1,则不含9.于是不含4(4 1 5=10),故含6;于是不含3(3 6 1=10),故含7;于是不含2(2 1 7=10),故含8.但是5 7 8=20是10的倍数,矛盾.若
中含1,则不含9.于是不含4(4 1 5=10),故含6;于是不含3(3 6 1=10),故含7;于是不含2(2 1 7=10),故含8.但是5 7 8=20是10的倍数,矛盾.若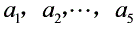 中含9,则不含1.于是不含6(6 9 5=20),故含4;于是不含7(7 4 9=20),故含3;于是不含8(8 9 3=10),故含2.但是5 3 2=10是10的倍数,矛盾.综上所述,n的最小值为5.……………… 15分★★ 14、已知有6个互不相同的正整数
中含9,则不含1.于是不含6(6 9 5=20),故含4;于是不含7(7 4 9=20),故含3;于是不含8(8 9 3=10),故含2.但是5 3 2=10是10的倍数,矛盾.综上所述,n的最小值为5.……………… 15分★★ 14、已知有6个互不相同的正整数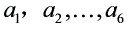 ,且
,且 ,从这6个数中任意取出3个数,分别设为
,从这6个数中任意取出3个数,分别设为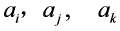 ,其中
,其中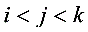 。记
。记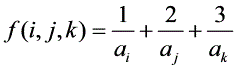 证明:一定存在3个不同的数组
证明:一定存在3个不同的数组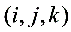 ,其中
,其中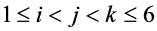 ,使得对应着的3个
,使得对应着的3个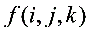 两两之差的绝对值都小于0.5.(征求答案)
两两之差的绝对值都小于0.5.(征求答案)
