请在下方输入要搜索的题目：

设有两个十进制数,x = -0.875 × 21,y = 0.625 × 22:(1) 将x、y尾数转换为二进制补码形式。(2) 设阶码2位,阶符1位,数符1位,尾数3位,通过补码运算规则求出z = x – y二进制浮点规格化成果。

发布时间：2025-06-23 01:50:54

推荐参考答案 ( 由快搜搜题库官方老师解答 )

联系客服

答案：解:(1)设S1为x尾数,S2为y尾数,则S1 = (-0.875)10 = (-0.111)2[S1]补 = 1.001S2 = (0.625)10 = ( 0.101)2[S2]补 = 0.101(2)求z = x – y二进制浮点规格化成果。(A)对阶:设x阶码为jx,y阶码为jy,jx = ( 01)2,jy = ( 10)2,jx – jy = (01)2 – (10)2 = (-01)2,小阶尾数S1右移一位,S1 = (-0.0111)2,jx阶码加1,则jx = (10)2 = jy,经舍入后,S1 = (-0,100)2,对阶完毕。

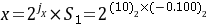
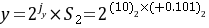(B)尾数相减[S1]补= 11.100 [-S2]补= 11.011[S1-S2]补= 10.111 尾数求和绝对值不不大于1尾数右移一位,最低有效位舍掉,阶码加1(右规),则[S1-S2]补 = 11.011(规格化数),jx = jy = 11(C)规格化成果011.1011D. 将两个正数相加有也许产生溢出

相关试题

教师资格证面试结构化题库选调生题库公务员考试题库题库软件公安题库事业单位招聘考试题库邮政考试题库及答案人文知识题库教师资格证试讲题库教师招聘考试题库面试题题库统考题库教师职业道德题库社会工作者考试题库公基题库社区考试题库教师资格证试题库银行笔试题库及答案国家电网企业文化题库遴选题库