已知a、b、c为三角形ABC中角A、B、C的对边,且a2-a-2b-2c=0,a 2b-2c 3=0,求这个三角形的最大内角.
已知a、b、c为三角形ABC中角
A、
B、C的对边,且a2-a-2b-2c=0,a 2b-2c 3=0,求这个三角形的最大内角.
发布时间:2025-07-06 00:01:40
已知a、b、c为三角形ABC中角
A、
B、C的对边,且a2-a-2b-2c=0,a 2b-2c 3=0,求这个三角形的最大内角.
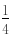 (a2-2a-3)=
(a2-2a-3)=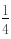 (a-3)(a 1),c=
(a-3)(a 1),c=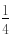 (a2 3)------------(3分)因为b>0,所以a2-2a-3>0,所以a>3,------------(5分)所以b-c=-
(a2 3)------------(3分)因为b>0,所以a2-2a-3>0,所以a>3,------------(5分)所以b-c=-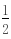 (a 3)<0,即b<c ①--------(7分)又c-a=
(a 3)<0,即b<c ①--------(7分)又c-a=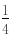 (a2-4a 3)=
(a2-4a 3)=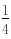 (a-3)(a-1)>0,所以c>a ②.由①②可得c边最大.---------(8分)在三角形ABC中,有余弦定理得:cosC=
(a-3)(a-1)>0,所以c>a ②.由①②可得c边最大.---------(8分)在三角形ABC中,有余弦定理得:cosC=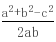 =
=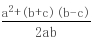 =
= =-
=-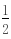 所以C=120°,即三角形的最大内角为1200---------(11分)
所以C=120°,即三角形的最大内角为1200---------(11分)
