如图,在正方形ABCD中,等边△AEF的顶点E、F分别在BC和CD上。(1)、求证:△ABE≌△ADF;(2)、若等边△AEF的周长为6,求正方形ABCD的边长。
如图,在正方形ABCD中,等边△AEF的顶点
E、F分别在BC和CD上。(1)、求证:△ABE≌△ADF;(2)、若等边△AEF的周长为6,求正方形ABCD的边长。
发布时间:2025-02-25 21:36:12
如图,在正方形ABCD中,等边△AEF的顶点
E、F分别在BC和CD上。(1)、求证:△ABE≌△ADF;(2)、若等边△AEF的周长为6,求正方形ABCD的边长。
 .[解析]试题分析:(1)根据四边形ABCD是正方形,得出AB=AD,∠B=∠D=90°,再根据△AEF是等边三角形,得出AE=AF,最后根据HL即可证出△ABE≌△ADF;(2)根据等边△AEF的周长是6,得出AE=EF=AF的长,再根据(1)的证明得出CE=CF,∠C=90°,从而得出△ECF是等腰直角三角形,再根据勾股定理得出EC的值,设BE=x,则AB=x
.[解析]试题分析:(1)根据四边形ABCD是正方形,得出AB=AD,∠B=∠D=90°,再根据△AEF是等边三角形,得出AE=AF,最后根据HL即可证出△ABE≌△ADF;(2)根据等边△AEF的周长是6,得出AE=EF=AF的长,再根据(1)的证明得出CE=CF,∠C=90°,从而得出△ECF是等腰直角三角形,再根据勾股定理得出EC的值,设BE=x,则AB=x 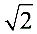 ,在Rt△ABE中,AB2 BE2=AE2,求出x的值,即可得出正方形ABCD的边长.试题解析:(1)证明:∵四边形ABCD是正方形,∴AB=AD,∵△AEF是等边三角形,∴AE=AF,在Rt△ABE和Rt△ADF中,∵AB=AD,AE=AF∴Rt△ABE≌Rt△ADF;(2)∵等边△AEF的周长是6,∴AE=EF=AF=2,又∵Rt△ABE≌Rt△ADF,∴BE=DF,∴CE=CF,∠C=90°,即△ECF是等腰直角三角形,由勾股定理得CE2 CF2=EF2, ∴EC=
,在Rt△ABE中,AB2 BE2=AE2,求出x的值,即可得出正方形ABCD的边长.试题解析:(1)证明:∵四边形ABCD是正方形,∴AB=AD,∵△AEF是等边三角形,∴AE=AF,在Rt△ABE和Rt△ADF中,∵AB=AD,AE=AF∴Rt△ABE≌Rt△ADF;(2)∵等边△AEF的周长是6,∴AE=EF=AF=2,又∵Rt△ABE≌Rt△ADF,∴BE=DF,∴CE=CF,∠C=90°,即△ECF是等腰直角三角形,由勾股定理得CE2 CF2=EF2, ∴EC= ,设BE=x,则AB=x
,设BE=x,则AB=x 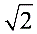 ,在Rt△ABE中,AB2 BE2=AE2,即(x
,在Rt△ABE中,AB2 BE2=AE2,即(x 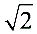 )2 x2=4,解得x1=
)2 x2=4,解得x1=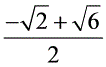 或x2=
或x2=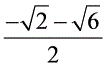 (舍去),∴AB=
(舍去),∴AB=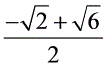
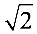 =
=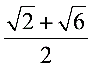 ,∴正方形ABCD的边长为
,∴正方形ABCD的边长为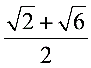 .考点: 1.正方形的性质;2.全等三角形的判定与性质;
.考点: 1.正方形的性质;2.全等三角形的判定与性质;
