已知函数f(x)=x-alnx(a∈R)(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程.(2)求函数f(x)的极值.
已知函数f(x)=x-alnx(a∈R)(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程.(2)求函数f(x)的极值.
发布时间:2025-06-29 14:52:54
已知函数f(x)=x-alnx(a∈R)(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程.(2)求函数f(x)的极值.

 .(1)当a=2时,f(x)=x-2lnx,f′(x)=1-
.(1)当a=2时,f(x)=x-2lnx,f′(x)=1-
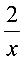 (x>0),所以f(1)=1,f'(1)=-1,所以y=f(x)在点A(1,f(1))处的切线方程为y-1=-(x-1),即x y-2=0.(2)由f′(x)=
(x>0),所以f(1)=1,f'(1)=-1,所以y=f(x)在点A(1,f(1))处的切线方程为y-1=-(x-1),即x y-2=0.(2)由f′(x)=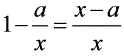 ,x>0可知:①当a≤0时,f'(x)>0,函数f(x)为(0, ∞)上的增函数,函数f(x)无极值;②当a>0时,由f'(x)=0,解得x=a;因为x∈(0,a)时,f'(x)<0,x∈(a, ∞)时,f'(x)>0,所以f(x)在x=a处取得极小值,且极小值为f(a)=a-alna,无极大值.综上:当a≤0时,函数f(x)无极值,当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
,x>0可知:①当a≤0时,f'(x)>0,函数f(x)为(0, ∞)上的增函数,函数f(x)无极值;②当a>0时,由f'(x)=0,解得x=a;因为x∈(0,a)时,f'(x)<0,x∈(a, ∞)时,f'(x)>0,所以f(x)在x=a处取得极小值,且极小值为f(a)=a-alna,无极大值.综上:当a≤0时,函数f(x)无极值,当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
