(文)在一圆周上给定1000个点,如图,取其中一点,标记上数1,从这点开始按顺时针方向数到第二个点,标记上数2,从标记上2的点开始按顺时针方向数到第三个点,标记上数3……,继续这个过程直到1,2,3,…,2012都被标记到点上,圆周上这些点中有些可能会标记上不止一个数,在标上2012的那一点上的所有数中最小的数是 .
=2025078=20251000 78,1000个点为一圈,转了2025圈多余78点,故被标上2012的那一点是第一个被标记数1的点(算作第1点)后的第78个点,显然在第一圈时被标上的数n是最小的,由1 2 … n=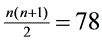
n(n 1)=1213n=12.(理)已知线段AB上有10个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1,称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),……,这样一直继续下去,直到1,2,3,…,2012都被标记到点上.则点2012上的所有标数中,最小的是 3 .解:从图中看出有如下规律:A点标记数除1外都是左行数,是两串数,公差都是12,一串是12n-2,另一串是12n 1;B点标记数都右行数,也是两串数,公差是12,一串是12n-8,另一串是12n-5,2011=12168-5,故点2011在B点,然后按左右左右数2012个数,在A点数到的数是9的奇数倍,即9(2n-1)=18n-9,B点数到的数是9的偶数倍,即92n=18n,2007=18112-9,∴数2007在A点数到,再向右数5个数,即到点3,就是点2012.
