在四棱锥PABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点F.求证:(1)PA∥平面EDB;(2)PB⊥平面EFD.
在四棱锥PABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点
F、求证:(1)PA∥平面EDB;(2)PB⊥平面EF
D、
发布时间:2025-05-18 18:13:33
在四棱锥PABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点
F、求证:(1)PA∥平面EDB;(2)PB⊥平面EF
D、
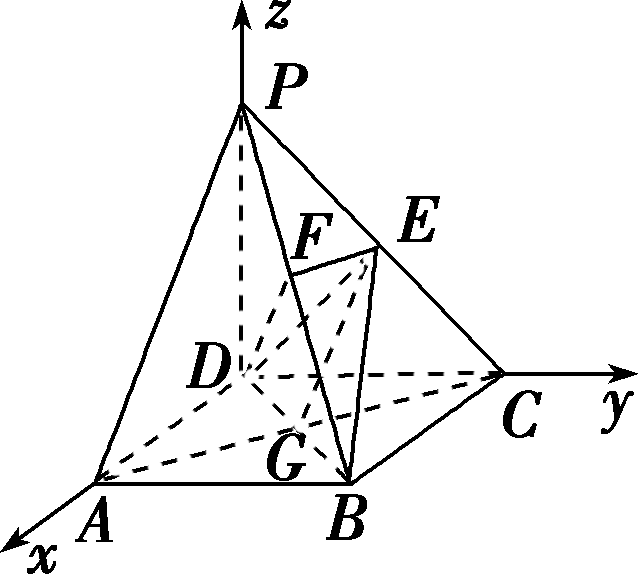 建立如图所示的空间直角坐标系.D是坐标原点,设DC=a.(1)连接AC交BD于G,连接EG,依题意得D(0,0,0),A(a,0,0),P(0,0,a),E
建立如图所示的空间直角坐标系.D是坐标原点,设DC=a.(1)连接AC交BD于G,连接EG,依题意得D(0,0,0),A(a,0,0),P(0,0,a),E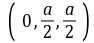 .因为底面ABCD是正方形,所以G是此正方形的中心,故点G的坐标为
.因为底面ABCD是正方形,所以G是此正方形的中心,故点G的坐标为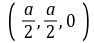 ,所以
,所以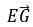 =
=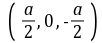 .又
.又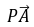 =(a,0,-a),所以
=(a,0,-a),所以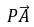 =2
=2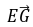 ,这表明PA∥EG.而EG平面EDB,且PA
,这表明PA∥EG.而EG平面EDB,且PA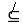 平面EDB,所以PA∥平面EDB.(2)依题意得B(a,a,0),
平面EDB,所以PA∥平面EDB.(2)依题意得B(a,a,0), =(a,a,-a),
=(a,a,-a),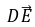 =
=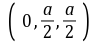 ,所以
,所以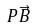 ·
·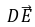 =0
=0 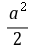 -
-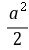 =0,所以
=0,所以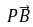 ⊥
⊥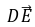 ,即PB⊥DE.又已知EF⊥PB,且EF∩DE=E,所以PB⊥平面EFD.[B 能力提升]
,即PB⊥DE.又已知EF⊥PB,且EF∩DE=E,所以PB⊥平面EFD.[B 能力提升]
