已知函数y=f(x),若在区间(-2,2)内有且仅有一个x0,使得f(x0)=1成立,则称函数f(x)具有性质M.(Ⅰ)若f(x)=sinx 2,判断f(x)是否具有性质M,说明理由;(Ⅱ)若函数f(x)=x2 2mx 2m 1具有性质M,试求实数m的取值范围.
已知函数y=f(x),若在区间(-2,2)内有且仅有一个x0,使得f(x0)=1成立,则称函数f(x)具有性质M.(Ⅰ)若f(x)=sinx 2,判断f(x)是否具有性质M,说明理由;(Ⅱ)若函数f(x)=x2 2mx 2m 1具有性质M,试求实数m的取值范围.
发布时间:2025-02-25 12:55:09
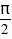 ,k∈Z.由于x0∈(-2,2),所以x0=-
,k∈Z.由于x0∈(-2,2),所以x0=- .又因为区间(-2,2)内有且仅有一个x0=-
.又因为区间(-2,2)内有且仅有一个x0=-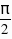 .使得f(x0)=1成立,所以f(x) 具有性质M;(Ⅱ)依题意,若函数f(x)=x2 2mx 2m 1具有性质M,即方程x2 2mx 2m=0在(-2,2)上有且只有一个实根.设h(x)=x2 2mx 2m,即h(x)=x2 2mx 2m在(-2,2)上有且只有一个零点.解法一:(1)当-m≤-2时,即m≥2时,可得h(x)在(-2,2)上为增函数,只需
.使得f(x0)=1成立,所以f(x) 具有性质M;(Ⅱ)依题意,若函数f(x)=x2 2mx 2m 1具有性质M,即方程x2 2mx 2m=0在(-2,2)上有且只有一个实根.设h(x)=x2 2mx 2m,即h(x)=x2 2mx 2m在(-2,2)上有且只有一个零点.解法一:(1)当-m≤-2时,即m≥2时,可得h(x)在(-2,2)上为增函数,只需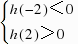 解得
解得 交集得m>2.(2)当-2<-m<2时,即-2<m<2时,若使函数h(x)在(-2,2)上有且只有一个零点,需考虑以下3种情况:(ⅰ)m=0时,h(x)=x2在(-2,2)上有且只有一个零点,符合题意.(ⅱ)当-2<-m<0即0<m<2时,需
交集得m>2.(2)当-2<-m<2时,即-2<m<2时,若使函数h(x)在(-2,2)上有且只有一个零点,需考虑以下3种情况:(ⅰ)m=0时,h(x)=x2在(-2,2)上有且只有一个零点,符合题意.(ⅱ)当-2<-m<0即0<m<2时,需 解得
解得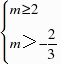 交集得∅.(ⅲ)当0<-m<2时,即-2<m<0时,需
交集得∅.(ⅲ)当0<-m<2时,即-2<m<0时,需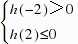 解得
解得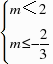 交集得
交集得 .(3)当-m≥2时,即m≤-2时,可得h(x)在(-2,2)上为减函数只需
.(3)当-m≥2时,即m≤-2时,可得h(x)在(-2,2)上为减函数只需 解得
解得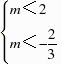 交集得m≤-2.综上所述,若函数f(x)具有性质M,实数m的取值范围是m
交集得m≤-2.综上所述,若函数f(x)具有性质M,实数m的取值范围是m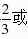 或m>2或m=0;解法二:依题意,(1)由h(-2)•h(2)<0得,(4-2m)(6m 4)<0,解得
或m>2或m=0;解法二:依题意,(1)由h(-2)•h(2)<0得,(4-2m)(6m 4)<0,解得 或m>2.同时需要考虑以下三种情况:(2)由
或m>2.同时需要考虑以下三种情况:(2)由 解得m=0.(3)由
解得m=0.(3)由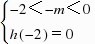 解得
解得 ,不等式组无解.(4)由
,不等式组无解.(4)由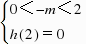 解得
解得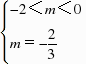 ,解得
,解得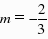 .综上所述,若函数f(x)具有性质M,实数m的取值范围是
.综上所述,若函数f(x)具有性质M,实数m的取值范围是 或m>2或m=0.
或m>2或m=0.

