设函数f(x)=ex-ax-2.(1)求f(x)的单调区间;(2)若a=1,k为整数,且当x>0时,(x-k)f′(x) x 1>0,求k的最大值.
设函数f(x)=ex-ax-2.(1)求f(x)的单调区间;(2)若a=1,k为整数,且当x>0时,(x-k)f′(x) x 1>0,求k的最大值.
发布时间:2026-01-12 23:58:15
设函数f(x)=ex-ax-2.(1)求f(x)的单调区间;(2)若a=1,k为整数,且当x>0时,(x-k)f′(x) x 1>0,求k的最大值.
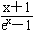 x(x>0).①令g(x)=
x(x>0).①令g(x)=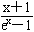 x,则g′(x)=
x,则g′(x)=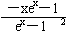 1=
1=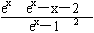 .由(1)知,函数h(x)=ex-x-2在(0, ∞)上单调递增.而h(1)<0,h(2)>0,所以h(x)在(0, ∞)上存在唯一的零点.故g′(x)在(0, ∞)上存在唯一的零点.设此零点为α,则α∈(1,2).当x∈(0,α)时,g′(x)<0;当x∈(α, ∞)时,g′(x)>0.所以g(x)在(0, ∞)上的最小值为g(α).又由g′(α)=0,可得eα=α 2,所以g(α)=α 1∈(2,3).由于①式等价于k
.由(1)知,函数h(x)=ex-x-2在(0, ∞)上单调递增.而h(1)<0,h(2)>0,所以h(x)在(0, ∞)上存在唯一的零点.故g′(x)在(0, ∞)上存在唯一的零点.设此零点为α,则α∈(1,2).当x∈(0,α)时,g′(x)<0;当x∈(α, ∞)时,g′(x)>0.所以g(x)在(0, ∞)上的最小值为g(α).又由g′(α)=0,可得eα=α 2,所以g(α)=α 1∈(2,3).由于①式等价于k