设f(x)=ax2 bx,1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
设f(x)=ax2 bx,1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
发布时间:2025-10-14 22:35:59
设f(x)=ax2 bx,1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
 则4a-2b=m(a-b) n(a b),即4a-2b=(m n)a (n-m)b,于是得
则4a-2b=m(a-b) n(a b),即4a-2b=(m n)a (n-m)b,于是得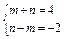 ,解得
,解得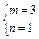 ,∴f(-2)=3f(-1) f(1).又∵1≤f(-1)≤2,2≤f(1)≤4,∴5≤3f(-1) f(1)≤10,故5≤f(-2)≤10.方法二 由
,∴f(-2)=3f(-1) f(1).又∵1≤f(-1)≤2,2≤f(1)≤4,∴5≤3f(-1) f(1)≤10,故5≤f(-2)≤10.方法二 由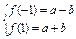 ,得
,得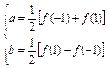 ,∴f(-2)=4a-2b=3f(-1) f(1).又∵1≤f(-1)≤2,2≤f(1)≤4,∴5≤3f(-1) f(1)≤10,故5≤f(-2)≤10.方法三 由
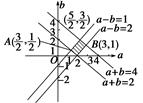
,∴f(-2)=4a-2b=3f(-1) f(1).又∵1≤f(-1)≤2,2≤f(1)≤4,∴5≤3f(-1) f(1)≤10,故5≤f(-2)≤10.方法三 由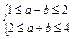 确定的平面区域如图.当f(-2)=4a-2b过点A
确定的平面区域如图.当f(-2)=4a-2b过点A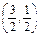 时,取得最小值4×
时,取得最小值4×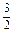 -2×
-2×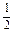 =5,当f(-2)=4a-2b过点B(3,1)时,取得最大值4×3-2×1=10,∴5≤f(-2)≤10.
=5,当f(-2)=4a-2b过点B(3,1)时,取得最大值4×3-2×1=10,∴5≤f(-2)≤10.
