=1 x x2 … xn 0(xm
=1 x x2 … xn 0(xm
发布时间：2025-05-10 08:08:32
请在 下方输入 要搜索的题目：
推荐参考答案 (
由 快搜搜题库 官方老师解答 )
答案：
相关试题
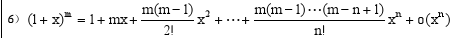
- 1.=1 x x2 … xn 0(xm
- 2.设m,n∈Z ,证明:当x→0时,(1)o(xm) o(xn)=o(xl),l=min{m,n};(2)o(xm)×o(xn)=o(xm n);(3)若α是x→0时的无穷小,则αxm=o(xm);(4)
-
3.(2)∑(1-x)xn,0
- 4.数列{xn}满足：x1=1，x2=-1，且xn-1 xn 1=2xn（n≥2），则xn=______．
- 5.若xm=3，xn=2，则xm n=______．
- 6.若X1，X2…Xn是来自总体X的一个简单随机样本，则X1，X2…Xn满足()
- 7.如果X1，X2，…，Xn是n个随机变量，则称X = (X1，X2，…，Xn)为n维随机变量．
- 8.、求极限: lim ( x2 x 1 x2 x 1) .
- 9.若X~U[-a, a](a>0), X1,X2,...Xn是来自X的样本, 则a的极大似然估计是
- 10.3.决定m,n,p使下列条件成立:o-r 13n 13m1m3 2)x4 x2 1|x3m x3n 1 x3p 23)x2 x 1|x2m xm 14)(x-1)2mx4 x2 1
