查缺补漏,以防万一。
查缺补漏,以防万一。
发布时间:2025-03-31 06:49:31
查缺补漏,以防万一。
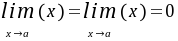 ,且
,且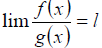 (1)
(1)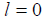 ,称f(x)是比g(x)高阶的无穷小,记以f (x) = 0[g(x)],称g(x)是比f (x)低阶的无穷小。(2)
,称f(x)是比g(x)高阶的无穷小,记以f (x) = 0[g(x)],称g(x)是比f (x)低阶的无穷小。(2)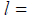
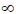 ,,称f(x)是g(x)低阶无穷小。(3)
,,称f(x)是g(x)低阶无穷小。(3)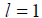 ,称f(x)与g(x)是等价无穷小,记以
,称f(x)与g(x)是等价无穷小,记以 (4)
(4)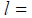 C,(C不为0和1),称f (x)与g(x)是同阶而不等价无穷小。(5)不存在(不是无穷大),称f (x)与g(x)无法比较阶数。等价无穷小替换定理:设
C,(C不为0和1),称f (x)与g(x)是同阶而不等价无穷小。(5)不存在(不是无穷大),称f (x)与g(x)无法比较阶数。等价无穷小替换定理:设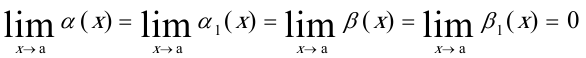 当
当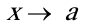 时,
时,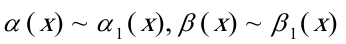
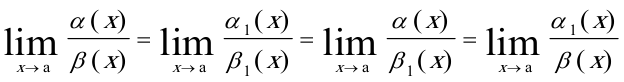 对称性:
对称性: 传递性:
传递性: ,则
,则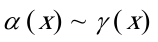 何时能替换的问题:整体乘积相乘能代,相加、减一般不能代,个别可以。
何时能替换的问题:整体乘积相乘能代,相加、减一般不能代,个别可以。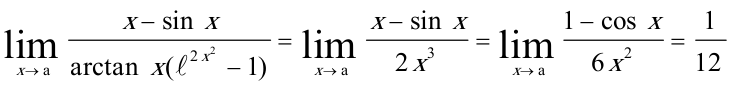 (sinx不能替换,加减不能换)
(sinx不能替换,加减不能换)
