函数不等式证明通常证明不等式的方法有:应用微分中值定理;应用单调性;函数最大最小值。例.证明
函数不等式证明通常证明不等式的方法有:应用微分中值定理;应用单调性;函数最大最小值。例.证明
发布时间:2025-05-11 12:30:07
函数不等式证明通常证明不等式的方法有:应用微分中值定理;应用单调性;函数最大最小值。例.证明
 上满足拉格朗日定理,存在使得;,两边取绝对值,。例.证明:当时,成立。证明:构造, ()则
上满足拉格朗日定理,存在使得;,两边取绝对值,。例.证明:当时,成立。证明:构造, ()则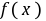 在上严格单调上升,,即,。构造,,令,所以严格单调下降,,故,所以。说明严格单调下降,,即,。结合前面的两结论可知原命题成立。例.证明,当时,有证明:原命题等价于:构造函数,,,,=()严格单调上升, >0严格单调上升,即,亦即,,即原命题得证。例. 证明:当时,。证明:令,,有且仅有一根
在上严格单调上升,,即,。构造,,令,所以严格单调下降,,故,所以。说明严格单调下降,,即,。结合前面的两结论可知原命题成立。例.证明,当时,有证明:原命题等价于:构造函数,,,,=()严格单调上升, >0严格单调上升,即,亦即,,即原命题得证。例. 证明:当时,。证明:令,,有且仅有一根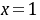 ,。 在
,。 在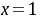 取极小值,,,,所以,,命题得证.例.证明:当时,证明: 原命题等价于:,构造,, ,所以严格单调上升,,即原命题得证。例7. 证明:当时,证明:令,,由得,,,;所以,当时,,即,即, 成立。
取极小值,,,,所以,,命题得证.例.证明:当时,证明: 原命题等价于:,构造,, ,所以严格单调上升,,即原命题得证。例7. 证明:当时,证明:令,,由得,,,;所以,当时,,即,即, 成立。
