已知函数f(x)=x2 lnx-ax.(1)若f(x)在(0,1)上是增函数,求a得取值范围;(2)在(1)的结论下,设g(x)=e2x |ex-a|,x∈[0,ln3],求函数g(x)的最小值.
已知函数f(x)=x2 lnx-ax.(1)若f(x)在(0,1)上是增函数,求a得取值范围;(2)在(1)的结论下,设g(x)=e2x |ex-a|,x∈[0,ln3],求函数g(x)的最小值.
发布时间:2025-06-02 03:35:54
已知函数f(x)=x2 lnx-ax.(1)若f(x)在(0,1)上是增函数,求a得取值范围;(2)在(1)的结论下,设g(x)=e2x |ex-a|,x∈[0,ln3],求函数g(x)的最小值.
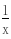 -a,(1分)∵f(x)在(0,1)上是增函数,∴2x
-a,(1分)∵f(x)在(0,1)上是增函数,∴2x 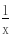 -a>0在(0,1)上恒成立,即a<2x
-a>0在(0,1)上恒成立,即a<2x 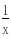 恒成立.∵2x
恒成立.∵2x 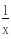 ≥2
≥2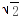 (当且仅当x=
(当且仅当x=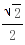 时取等号),所以a<2
时取等号),所以a<2 .(4分)当a=2
.(4分)当a=2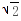 时,易知f(x)在(0,1)上也是增函数,所以a≤2
时,易知f(x)在(0,1)上也是增函数,所以a≤2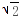 .(5分)(2)设t=ex,则h(t)=t2 |t-a|,∵x∈[0,ln3],∴t∈[1,3].(7分)当a≤1时,h(t)=t2 t-a,在区间[1,3]上是增函数,所以h(t)的最小值为h(1)=2-a.(9分)当1<a≤2
.(5分)(2)设t=ex,则h(t)=t2 |t-a|,∵x∈[0,ln3],∴t∈[1,3].(7分)当a≤1时,h(t)=t2 t-a,在区间[1,3]上是增函数,所以h(t)的最小值为h(1)=2-a.(9分)当1<a≤2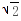 时,h(t)=
时,h(t)=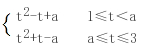 .因为函数h(t)在区间[a,3]上是增函数,在区间[1,a]上也是增函数,所以h(t)在[1,3]上为增函数,所以h(t)的最小值为h(1)=a.(14分)所以,当a≤1时,g(x)的最小值为2-a;当1<a≤2
.因为函数h(t)在区间[a,3]上是增函数,在区间[1,a]上也是增函数,所以h(t)在[1,3]上为增函数,所以h(t)的最小值为h(1)=a.(14分)所以,当a≤1时,g(x)的最小值为2-a;当1<a≤2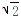 时,g(x)的最小值为a.(15分)
时,g(x)的最小值为a.(15分)
