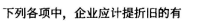试计算图中A、B、C、D和E点的坐标。<img src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAU8AAAEcCAYAAAEw0AY9AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AADtPSURBVHhe7Z0JwFVz/v+fQbRppFDSKlqMVBNiUv5G0xBlYhJFaA9ToVDRGFkq2eI3iamZlGJsSVEiYsgSRUQl7Stp1arv//0+z/f7dJ/b3c69Z7+f13u+45xzn+fp3O/93M/5rp9PgQoJcqNO4/mNHnfccfqoOKNGjdJHiXH9RgsK7P0TNWrU0EfFcfxG69evr4+yZ+y8sfroIClv9FooFbt27VLDhg3TZ85QkOSWbNXomjVr1DXXXKPPkrMC2gdlyo8Q2QYZ7rjjDn1USNobTWT8/4RyJfbTWggtgt6BkpH0Rt977z19FAwS3midOnX0kb+sXbtWHyW40TenvqmPgoWtL5OfFLvRn376SR85ywfQQCgXUtZoVehJ6AYoF9ZBf4FyIaOPfgNURBf9X48pulG7z2SvKbq7ffsOfZJUqFDhkNKpQqfCUtAp4esJS6eYkuD1unXrpnWJRTd6xRVX6KNgUnSjTjcunCbYhhlDOG90+/bt+ih4eFKjd0J3Qbng2Ue/FcqFpDdK35YKeFJ95A1pa3Ty5Mn6yF8y/uj5iJ0yZYpq2rSpvuItWdnofVAsnTt3VsOHD9dn7pDVjWZqn+wYLly4MOsGz+LFi/VRljfqB3KjsfwM5YqtG30WMrSEnoC+hEgbyE1s3ejn0E6I/AqR7RBZALmJ2KjTyI06jac3umjRIvXJJ5+oxo0b6ysHmTZtmj5KjKs32qdPH32UO7Zu9I033tBHibnyyivVzz/n7twTkVONtm3bVh85y+zZs/XRQWzdqFvDPldD6Uj7L/Pj/vTTT/VZ4cgcH5+5wN/n3zG0g+Jp3ry5PirEnSpygJdeekkfFeLZjd4O2cHM4L0NEc9uNNlEVzJS1qj5ttn9o5kwALJDxh89J6ic4CGIOHajtWrV0kfFGQTlwg6I33DXajQhOUxsDIHskPWNzoZywdEvUyzjx48/ZKy9oEJB0Rh+/GspS6cKqtTrpVKO4fO/seT20eeAazXqNCdDdkh6oxs3btRH7uDYt56tbzfx1j3lgNyo08iNkp49e+qj4twB2cXTGj3ssMPUhg0b1B7ILr589PFzRpl0+lx/Mu2F4hkKpYMdwqpVq+oz+12Rk08u/iTLqkb9IKsbvQjymqxutNhimDSsgZzA1o2y8XwFZHgX8gpbN8rx+zegeL6C3CbaX6awYKaWvCTSFfp3yGsiXaHxsEVy1FFHqSZNmqj169db5ZJLLlG//e1v0051ZEqkKpSNZ1bahAkT9JXseeedd9TWrfaXFYWqQkePHq1q166tdu/era94Q7JNOInIukJfh1pAqbAzL7Zt2zZrnKx06dL6SnCoBWVK1hXKht5/ITu0bt1a9evXT5/Z40SI9IP8ZMaMGfooMY595atXr275L478usH/IHIv5AZcQmQWyKQj0Yp1Q9YV6tbErV/MhzIl1Xu3VStB2d7kFHwOZAMr9LvvvtNnSi2GDBlVqBMbJ73EjRncWOJHw2LJ+F/OdU26lwSyQi+77DJ9VJzBUNCxO1BsF9sVyt2+6fgaWgV1gzgu+zAUFAJXoamaBQazbXoOtBnaCAWFQFXo2LGH7roPG4HyoVdddZU+yo3+kF/0gdzEVoXu3XvofJdjFK6qc51AfeWj0AMKRTs0TATuKX/sscfqo3ASuAolI0aM0EfhI5AVSqpVq6aPgo1ZOLIaIoGt0LDwLcQeGxdOl4ZCU6GvvPKKPgo2obPQjz76SO3ZY3912/MQrcltQv+V37lzp7WIjRacejTbGw+TVz6U4QtY6Qxl4Bahb9ini0qYLVw4e9ZZZ1mLaKdOnaqvpkd6Sjny0riXPO0y89966qmn9FlxPK3QRAuNo0YkLNTrCEOp8L1C74di4eh/mHG1QidA5DGIML6KWQHCuWwuLl8ORYlIfOWDhFSow0S2Qq+D3oe8JtIVmmjLittEtkL/CvmB+FCHyZsK5Tp5dhljd4Cw8Lxs2bL6p3In0hXKVdVVqlSxjhnHPZOtM3Y2KCTC1QrlRgSv4BaYli1bOjYsmC6gbjJcrdDYndNucNJJJ6mBA3OL8p+Kjz/+WB9ljqsVyq+cU3D3BX1gu3aHxiQLEq5WaC5jlAzQVapUKfXtt+7PQaVj5oyZ+ig9rlbo8ccfr4/S88MPP1hf4Xff9WZzu90Pu2LFivooNa5WaCofOnHiROtNvfbaa/qKt2RSoadDsUyfPl0fJcezCmWiJ76J1asLV3dkw4OQU6Sr0BegeN58M31CItcqlDvqyh9d3pGm0xiIPADlmnjAkKxCP4ZSBS749dfUu+0cq1DeIMuSJUv0FVjoHGebTblGMY0lvkJvgcgnEBkOJaJy5cr6KDE5VSh3k3Xv3t06TvTJVZ9T2GxyIqSrE8SGhS3oXvytm3x0nGVYCmVLVhXatWtXNWnSJH2WHKct1EkK+hx8607k4DPYrtB69erpo/RU/STAFXpr4Vu/G7ILm3jJsFWhP/5Y+LXIFLe7nrlAH5rt3qpY/9sVil0AZ9tC7RD0Cs2W2N/l/v0fIENGfzWbpYskqhUa+5VnKKNdkCHtX+0wo4M+sk8+VGg8Kf+q2Sef7Wo2Pyo00zAXnldofAbdw6GJkB3EQmNwInWGVKimffv2+igxj0KZ4FWFroVGQ3bwtEIHDEi9Rp03n0mMS7HQDHkOIuniHHtVoedA7KObfnomeFahmYyy/wf6FEq3L33W8bP0UbSwVaGNGjXSR/boCcUzp+ocfRQtbFVoLondb4Ni8aNCM22H5oLjPjQV2yCDWKjD5H2FDhmSWVah+Pw4iUrFChXV3HpzD+bUZ6ncSe08ZWfCn8+5xObhNyXRzyUonCI2efp53qBBA/1OE+N4hWbKIc2mzNcLBBrfvvJBbtjnQl5VaOCe8k7mE/WjQg9AbmOrQi+44AJ9lDvylQf9+zsXYk0q1GGkQjXDhg3TR7khFaphJAUnkAqNwQkrLVOmjD6KFr75UC/5BVoPeUHWFdqjRw99FGw+h7wkJws99dRT9VFwORXyMix8zl/5ZEm+gwKT5XmJIz70jDPO0Ee5kWs+8CDg2EPJJPfPdxyrUMMpp5yij+zhVew7t3G8Qg1257abQVHAtQo1MEAgt0WbJFVRx/UKNbRt29YKM8zNXVzOw439ZvfZzKjMfwDPKjQdzHpISz7nnHNSRjgMOq5WKJOs5Pqweeihh1TNmjUt15ErgRuxtwsrdB6UilOgUZAddu3aZcUOPeKII5KGlvQLVyuUvZR0qSGZd8nOyrhUMMc+m20cGly4cKF1jdsFV61aZR17QaoHb84Vmikm/5Ib8A1OnjxZn7nLq6++GowKDVKMTzfxrEKj0ktKRyQqNEhtXM8q1M3k+VdCQSH030M+7IZCQcH3Cn0KMtwKhR1XKrQRRNpB3Fh6JkSaQCaJAOMxk/egKOFKhZrstB9ApC9EWLmmgW8SNI+EDNkEAwgarn7lX4J2Q1Mhwv+aKOGxzILIDCjshP6hFDSkQh1GKjSEXAi1hvIBMdAQwojy5E0o6oiBhhAaKLtDXi+R8wMxUCHQiIFGkJUrV1pROUaNKj7LzAC58SXoiIFGhA8//FAdc8wxqlKlStbaaE7KsjDViR0YX5e/f+KJJ1p/7/vvv9ev+IMYaAjYvXu3WrNmjWrYsKE66qijrFVhzDnhJZ988okqXbq056vRQm2gJ5xwgj4KN/v371cdOnRQZ555puX1HnvsMbVjxw79ajDhPY4ZUxgH301CbaBh2kM6dOhQy/i4TdOEqI8KmeZHyYZQG2iqxW9eMmXKFDV48GDrfpo1a6ZmzZqVU2C2MLJ8+XL16KOZRT+1gy+f8NvQT1Au0Ai8MtAvvvjCyqnIDgg7DwsWLLDWVQvF+TfUtnXbtGln7OC5gTaFSA8oV5x4xG/ZskV99NFH6txzz7UMvm/fvuqVV17Rr0YTJ7/Yr0KJ1qeasPK54rmB3gA5RaYG+sADD6irr77a+mDuv/9+yyDdInZDxn+h26GgkauBcrsSjTLdwmknvgieG+giaBA0H8oVbifl4+SRRx6xKuP0009XHTt2dPQRY4cVkInxTZjljWyBgkQqw1kJxUatvx6KzdHF1akfQpmSq5F6bqCZcPTRR1tvbPHixerLL7+0OiHcQ9e4cWM1aNAgtXbtWuvnqkwpTB0dFLhZiBFPzAfIlAlfQ14H7UhHKqPZBC2BNkAGk5lvP3QNRCPOlO3bt6tevXrpM/sEwkCZm3LRokXWjlmG3WEFsowbN07/RGKCmORuOxQLvWrQKCif/GNndsO90PeQwRio4R+QHZ5//nnL0WSDLwbKXjDHA1988UV9JTvKzylvZTikSmqZthFlXstHxdaDqZui115I/rE7lXg2nmwf9Z4ZKHvJThPkNKFBJjaFqcGsMXWLqVOnqmXLlumzzHHVQP/v//4vo3y02VK1ghhoNhQcXvixs/MzAPKCmTNnqueeO9iBzBRXDJRtSS+Iarhcwi2E7JDU/6y+VUp9VqroOGmpn1kpaFugzjvjvISv2S2ZYPoULMwDEo/Zlp4ou5ljBrpz586Mb9gpomyg8QyBnCLb9mAucPIj2fSveW8cgozHkTu99557rRU5XpNPBsrOjlP4YaBcppcstNXNEENlnwfFk/Oddu3a1fpvZYjDE16SLwbKXDtRNtBUZH2nXDyRKMH8YdCRUGxWP7fIJw9qwl84QaQNdO/evVZw1XScD7GR7yb5ZKBO9rYja6D79u2zIkjaZQJkZ3osU6JkoDsgEzN2I7QQMgGCiBhoBmRjnLEw1FVNyHAnNBwy3APZWScaNQ/6HfQYFIs5FwNNAzdr5Qqn2RiUOXZJ2u8hwhVOpCuUKfnwiO8GETHQFDCGsRNbGLiMKzYcmwnTRuhNySVQppxY9UR9FH2cNNBLLsm8jp3CVQN1Kh/fRxCHTOZCDMb4BRS7LpRxAzNe/fM5/ncu/m+uPo84ThqoH7hmoCNHjrQ6R16TciU6M2HtUWpO1TlcfqMSxMiMFO9DTo6D+oFrBupHeyUWrlDnB5QIy0DzAKcH6v0gsgZqYPj0+Cjh+WKgRAw0AY8//rhjmc+dxOz7ea9qiojs3AYUofgIQdx8ZwdXDHTIkCHWzFFQKVe9nD5KwW0oqdONhQI3M6XEwtReLH369FFz56I7i+IErhgo95E8/PDD+ix45NNUZz0ozLjWBmVQq6CSTwYqbdAkBKWTlIh8MVDpxaeAf5jBUYNIPnlQGahPQVC9qBhoeHDVQPnH/Q4FnQgx0PDgqoGSa6+9Vm3YcDAcShAQAw0PrhsocWrRiFOIgYYHTwyUJNrX7BdioOHBMwMll156qT4SvEIMNAtOO+00fSTkyn3QZugriMeEubdNUAMx0CwJ8kB+lBADzZGTTz5ZHwnZwBVa3GFgYBBZ7kcyM0hioA7BNHqC84iBOsy0adPUCy+8oM/8g4kMooAYqIuwnZpNbEgn4Ea9KCAG6hEMqM+xVAbXd5MXILbfTLSOsCMG6hOrVq1SDRo0UNdcc03CN/DOO+/oI3uUgr6EooIYaMBgsAg2DUypXbu2uuuuu9TSpUvV5s2b9U8lpxUUJcRAQ8zs2bPV2LFj1QUXXFBo0DcXqEtaX2J556Cntc6En6F+UJgJtYFOh0zoGy9gs+G2224r8s7XX3+9GjBgQCCXFBJZUe8zDD1Icv0Q7oII/44TnSN6XxamV2zdurW1mosGzajS9NheIgbqIzRQhg/vA+VCe4gcA/nB6tWrrTYy28ssTOnI8sEHH1glF7qHfJP/yy+/nFUAukAY6LMQ81zOhOzC1CUMQGbExRbsvfO/sdeDIN4TtUbrobceskrBkfCPlVHOQDmiwAqv3uDyBqpBp4OlzOtlip0nLQ2CV84///yi5lT79oVOJFPC/dxIwpNQGFmzZo1666239Fm02LRpkzW7aJdIGmjY22vCQSJroGGcQXIjjn/YiaSBngj1h8LEvdBASChOZJ+FP0BhggYa9p66G0TWQDkqIISfUBko09Q4zdeQyTQSi0nwcDUk+EeoDHQwZJgEPQwZnoZi0wVynJGPeXY8YjOL8Jj6HiIcM+VUayL4+1utIPiCX4TKQLlgggsnCGeNuBjZZAUZA90BxcLXOMfP15LREjIzUI2hWF6BVkOCf0S2DSpEAzFQIdCIgQqBRgxUCCxinCGDCc0+hx6Hoo4YZ8gwoxVloagjxhkyjHHGD6NFETHOkGGM00S5izJinCHDGGc+rG8V4wwZ30I/QVEJ3ZMKMc6QwW3GzO6cD4hxCoFFjDOCjBs3TpUtW1Z9++23+opSW7duVePHjy9Wnn32Wf1qMBHjjBjvvvtu0dZdGmilSpWs7ck9e/ZU69evL1bWrl1rvcZy+OGHq0mTJqlPPvlE/yX/EeOMAPPmzVP/+te/1DHHHKMaNWpUZJxVqlTRP5EZDOfzyiuvWJGv+beGDx+uX/EHMc4QsmjRInXnnXeq6tWrq2OPPVbNnDlTLV68WL+q1Jw5c1SdOnXUunXr9JXsWLlypfX3+e+4HZ81EWKcIYDBGf76179aKXxKlCihZsyYkbPh2YXNAkb88JLQGucvv/yij6LFgQMHrM5Ly5YtVf369a3H84QJE9S+fcEYPipZsqS6+eab9Zm7hNY4r7vuOn0UbmiMjEXaoUMHyxDbtm2rHnvsMf1qMNmyZYs6/vjj9Zl7hNY4GcIwrDBSXZ8+fSxj7NGjh3r00Uf1K+GiYsWK6uuvv9ZnziPG6QHPP/+8FXqcxti9e3crNHlUuP/++9WXX7oTxz+0xtmlSxd9FDxGjx6tbrzxRssY27Vrpz7++GO1Z88e/Wr0GDZsmPrmm2/0mXOE1jgHDRqkbrnlFn3mL4z4S0NkSu9mzZpZwVV37dqlX80PGFzXaUJrnDQGGqjX0OiYZKFUqVJWPtFzzz1XLV++XL+a3/AzcRLPjZPpoRm4gOG5c4EVMXCg+5HbOJ74xRdfWNOAJ554otWrXrBggX5VMHAZ37+hy9tcrq/kjufGeSW0Cso19Msll1ziisdiQP4LL7xQ1a1bV5UuXVrdc8891nx1VJg/f35WEYlTwdBBN0KEM0kcsHcCT43zR4ipoAm/abngVG/9xx9/tB7NNWvWtLwx55ajzMKFCx0LBb4TKg3dCsXC5taSJYWfcy54apzrIafI1jjZZuRANxc20BjHjEkeVymKOGWc9JbcKpIsQ92RRx6pj7LHU+NcBzmFHePkz9IQ2WbkuJybMBiYgR7lGyhIOGGcNEgaZqodoHPnzlWff/65PssOT41zP3QfRPhIyIVkxskxxjvuuMMyRj6u+/XzNrXftRAZD5EuUJBwwjgfgV6G0sF5+FzwvENUD4qNvZktnPYjnPpjdjYaI//L1d+//vqr9ZrX8H3dDpEJELkOChLpjPMq6EyI7IZid3n+C+oIZQpHOd5//319Zh/PjTNXuL2gadOmljG2atXKWoSwf/9+/ap/MMHXu5BpgxnjDFpo8HTGeQ1UCTLEBun9A2QHOony5cvrM/sEzjiZYJWGx3FF8sYbb6gTTjjBmoFo3LixtbWA3DigcOgiSDAY7XEQMY91ux+o26Qzzp7Q2ZChF2Rgn+F0yA5s52dLoIyTHpCGaUqNGjXUd999p18tTte+wVz4cTNEfoE2QLOgIJHOOBkbvw1kiDVO8iJkB667HTIku+gkgTBObju4+OKLLW952GGHFRlnKoJqnCYiBwmaYZKFC2Cc/0v9WP8TZIg3TtNcsUO2HSNfjZOLJI444gjr0c1FtwbuiUlHl77Fe8F85FCM+U59DOUrwyBTD6ZetkNk9Vur1VtQMlpACyD+PEdXLoE2QoSdvWxyKXF3Zzb4YpzcgtCiRQt9lh29+vZS/9TqAZXUYu+SYq/SvJ5vqgOZejD10gjia3cvvjulR58IOQ23mIwcOVKfZY5nxsm2B7eqXnTRRfpKbgT1sR50Fr6Lx3oSz8nsJW7AJYTcumwXT4zz8ccftxbdOokYZ3YkMk6e2+3o2CVdHyIRrhsnB8udWAQQT9d+YpzZsHB2ceOcAXGM1m0CZZwbN25UFSpUcG2AvGsXMc5sWPgVjPPtQuNkW92riHWBMU7G4enWrZs+cwenlszlG6tXr1az35mtRkBewbW3yYYHOUXK1JHnQfE4bpy9e/f2ZG9P1I2T442tf2qt6n9W3yqVPqtUdJywTEKpn75wa0nNATVVo/qNEr5up3DjXjqWLl1aZJjJvCfbu8xfGo+jxskdkZs3b9Zn7pJvnvMNyAm4z3zWLG8nB26//XbLME8/PfHU59+h1lA8jhkngwRs2rRJn7lPvhnn65ATOLFkLhuSeU0yE+JqqHgcMU52fmicXpJPxjkH+gxygiAaZ7JhLEeMM9U/7Bb5ZJxMTtAVcoKgGSdHC0ZDHDmIJ2erKtGxhD7ylnwyTq4T4JSkEwTRcyYjJ+NkYAFyP3QP5CX5ZJxVobqQE+SFcXK4iJFvDVzCz4UGX0BekE/GWQ2qDTlB5I2Tw0WJBtmfgWigiYYFnCafjHMHFLurMxcib5yp/qGnIBoo5Sb5ZJxkOuQEkTbOTEIuPwG9ADE3uFuIcWZHpI3TzqpmrqaeBrmBGGd2RNY4swnQxOVYAyGniZpxciuFYaFWLGKcafjjH/+oj+xzPeQkUTNO00avAhnYwWS4SCLGmYLnnnvOSr6ULdwsxQ1X70CEC17bQQYu4bKT4D6Kj/UHIaasNnwJ7YKIGGcKkq0osQODixoPYSr7c4hMhS6CMkXanNkRSeN0IsQ1d/aZODzkO2gRRDiOtxzKlHwxTlM/YpxJuPTSS/VRbjSB5kGGDpCBxhn7SEtH1IyTkTbMHvNYmRCKYpxJyOYPJ+I/EDf8G7g838A26HNQpshjPTtWrFhhRX/zGleM8+eff1ZDhw7VZ7kxBmJMeEJDfBviHhJyLmSnR/94z8eVjVZA6HHKOP3CFeNkdNoXXnhBn2UPs2f8DzJDIzzmIpHYrBqMGZ8pI8qOUKq/PskDxDgTkGvYGLv0hrZBKUEzrG8/HTfy+8L/RJ33oDDjinE61d60w1woZSoYNFv79tDGWRjFO9KUgLimM8xExjgJV38/DSWjb9eDEXejDtdyOrXY2C8cN85ly5Y5nlDJLsk6SflknLUgMc44mM2MSUf95k4onnwyzvlQTSjMOG6cGzZsCExucPbuY6MG55NxfgAtjFulFDYcN87q1avro2DAoSeutCf5ZJxcNONUxA+/cNw4jzrqKH0ULLh6Z3CXNLmM7kLJfXg2MLwJhRnHjZNZc52C4RCdKlUrVFUFXQrUdRWuU50qdEpcKqLU6aReK3hNtajQIuHfCVz5I0qnxKXciHLFr52Nkuhv5FDq1KljZUtm4TELo1Gb1/fsyT6OZ6CN02luuvEmfZSCxSiPFR6GHba53YbJx0455RSrMHclC8OlO0FeGWfahR/O7wzxFZm+jCNoHaJY8mlV0mLIzZ2sXuC4cTJAaFDJJ+P8EAp7XiXHjbNWrVr6KHjkk3FyCK0GFGYcN86gzBAlIp+MU+bWE8C59SlTpuizYCHGGS4cN06maSlXrpw+Cxb5ZJzdoNht1GHEceMkYpzBQIaSEtCgQQN9FCzEOMOFK8bJR/ujjz6qz4KDGGe4cMU4OZ/asGFDfRYcxDjDhSvGSQ477DB9FBzEOMOFa8b56quv+hIlIhVinOHCNeNku/PCCy/UZ8FAjDNcuGachMuogoQYZ7hw1Ti5rs+JSHNOIcYZLlw1TlKpUiV95D9inOHCdeNkVuD+/YMRoEiMM1y4bpykRAl/cl3G06HDwdie+YAYZ4bUqBHutYVhRIwzQ/h4v+mmDDaYCRnDFIIGhok0oSINYpw26N27txVYVnAGk8ihOmQYDjH0NhHjtEnFihX1keAEjAnFuEiGz6CdEBHjtEmfPn0C03uPOmKcWbB69WrrES/kBh/hXPFeBxoNkfHQRoiIcWbJunXrpIOUI3+HDL9CYyEmdxDjdACGSxQDzY31UDwm24gYZ45s3LhRDNQlxDgdgI/43/3ud/rMf5h5NwqIcTpI2bJl9ZF/HIDuhqKAGKfDHHnkkWr5cv/SrP0M0UCjgBinC3ANaJs2bfSZt/SBooIYp4vccMMN6u9/Pzhc4jacDjRTglFAjNNluJq+Zs2aatSoUfqKe9AwObAdFcQ4PYILRrgn6cwzz1Tvv+98UFSODdI4zRhhFBDj9AFmiDv66KMTbj3eunWrWryYgd3tsQGK0iOdiHH6yMKFC1XVqlWtfUrHHXecmjdvnvWGWLZs2aJ/KjOYGvtZKEqIcQYIY5im1K5dWy1dutQq6eCcdNQQ4wwY3K/EN7V7d2HbkYFsWRgeh4WpSVg4r89iqAhFDTHOkDJ27FirGC973ojzVLt27dSOHTusEna2Qa9CYSZvjTMZw4cPt4ox2s6dO1slbFSDGHo7zITWODn/PQzyittuu0317NmzyGgHDBhglaAiMeF9BP5MLYdegXKBC3THQG9B2WA8KyuyVKlSltcNQuDc3pAYp090hNZAz0O58C70LZSrkRvYXv3pp59U69atrWI8Ldu306d710GZC50EhZnQGmczqCaUCy9C3Ea7BXoPchOODHzwwQfqrLPOUo0aNSoaPZg6dWpGQ112YVLWb6AwE1rjvBoiT0PZsgtifsgPoGmQH9AwR44caY3JVqtWzZr5qlevnmXIzMCbLXxvM6AwE3rj/A+UC72gd6D/BwWJTz/91FpDwJmvypUrWzNh11xzjTUrtnLlSutnuM2aH2CTJk2s83jegMIKO6B8b40bN9ZXMiMQxvl7qDHEaUe7LIAYiID6CloG8b/mWlDE++R9LYXYvv5w54fqobceUt2e6KYKSqEtWw/ldwXqN7/5jZVep0Gn4qXKiCqHXDuknI3C3w1QYbILfilpnHa9ZyCM00mugULHTqVqVayV1QcYBrinTIwTnAuFlTFjxuij6JHNe4uccYZ9JkU4SOSM8xxoCiSEn8gZZ1PodkgIP5H0nJWgsBH2lNVuEEnjRL9Qn4WHSyChOJEzzmshLjELG9IUOZTIGSeZDIWJORBXUsXGhRciapxc5RQmzLz5PyHhIJE0zg5QmGgFkVMh4SCRNM7vISH8RNI4M4VL0W6FGOY6Hj5iG0KCf4TKOJ1eNtYd2g9xBX08XEH0JST4R2iMcwXUEjKcB5nAsF2ggRCXpRn2QNdBhHE6yUroCS3C7BVkAJQI7kcS/CNUntPMmTMg7EzoFoiYRcockjHQeEl5yEAj5ZYHiqQzTm4fEfwjlMa5F6JXuwMiZggm1jjbQyR2fSezoS3WInysE+5ujGc7xG0fgn+EyjifghhBjivJyV3QPojJpMg8yHA9RFLNWccaHwN/xQ6C/w0K+6aysBMq4+TmNcMkaCpE+N8foLehWPgz5CMoGWY2iW1ado4M7HyFfVNZ2AmVcQr5hRinEFjEOIXAIsYpBBYxTiGwiHEKgstwCLQr1BPiGHvsqJAQXsR5CoLLrIW4BIRw+Px0aDUkhBtxnoLgMpyDNOvkyJ3Qm5AQbsR5CoLLxDtP7gcX5xl+xHkKgsvEOk8GS24Dxa+mE8KHOE9BcJlVkFkLzzHPGyBueRPCjThPQXCZh6ELIQZOSrVPQwgX4jwFQRCyQJynIISITZs2qfXr1+szwU/EeQpCCHjyySeLEuSZ0r9/f7V9+3Y1efJkddFFFxUVph+N/9lkpXnz5sV+l7mF+Td37typ/2UhGeI8BSGAHDhwwCrTp09XJUqUSOj4WG6++Wb1v/8Vhq1zgpdeeslK2j506NCif6Ns2bJWDmyWiRMnFt1bviPOUxB8hBltmbCeTtA4q9/+9rdqwIABVqHzJHRa5nVT7rvvPus1L/nwww+L7q1q1aqqUqVK1v2zZZxviPMUBJdg64ytuAcffNBqtRmnxxz1119/vVW+/vpr/dPhZsmSJdb7KVmypDr77LPVP/8Z/dRG4jwFIUvWrVunnnnmGas0a9asyDny+NJLL1XXXnut+vnnn63xw19/PTSxS5RZuXKlatOmjapSpYp69NFHrfOoIc7TB/r27avOOOMMfSYEkS1btqgpU6ZY5eKLLy5yjKeffrpq2rSpVe644w61ceNGqwjJ+emnn9SQIUPUaaedZtXhf/5TmIok7Ijz9IGuXbta40WCfyxbtkzNmTNHvffee6pOnTrq6KOPVuXLl1ennnqqVXr06KGWLl1qlf37JYSck7DeOVb6xBNPqBUrVuir4UOcpw+I83Sfb7/9Vn355Zfqv//9r9V1ZKlcubI6/vjjrfLII4+oefPmqc8//1z/huA1P/zwgzXpxc/jm2/Cl4ZJnKcPiPPMHY6hsTzwwAPWBAzLsccea01YHHPMMerFF19Ub7/9tpo/f77+DSHIcGkUH24LFy7UV4KPOE8f4LKUUqVKWctPhEPZvHmzVThje/7551uFDjF23PH555+3CrvfQnS466671AknnGDtpAo64jw9ht0TtpLoBAYNGqSv5hd79uyxCtcKXnHFFap169ZFjvHkk0+21gyysNst5B8cTmEvYty4cUoFeJGCOE+PmTVrVpGjiLLz/PHHH1WvXr1Uz549rZajec8XXnihuueee6zCWVhBSMS+rftU8weaq4K7C9SB3cHczRR557kcOgvqATH9QTNoO+QXM2bMKHIkbHmFlS+++MJafsLC1qJ5Tx06dFC9e/e2nKMQDNgF5kJ9TtAEnXVQA4gJ88gvW35R55x7jrryyisDtyU00s7zV4iJt/4BGRhTcRPkJ3Qu1atX12fBg7tFRo0aZZUGDRoUOcZWrVqp9u3bW+Xpp59We/futYoQbDgJw8/vrbfe0leCxWzoRghWpm6GEsGJwXLlylm2GRQi7Tz5FDNPMMNO6ADkJ37PtjOQxKRJk9S///1vyyD5xSpTpoy64IILrDJixAhrZwyLEH6C6DyZPfRs6DcQneZgKBP+8Ic/qN///vf6zF8i7TzXQ9dCQcNt5zl79mzrizJ8+HB15JFHWuXEE0+0WpEsr776qlq1apVas2aN/o1wMgVaAgmpCYLzZIOFKUiYu57O0mgQZJezzjpLXX755b6HzYu082T3/HyILdAgkYvz5G6XTz/91Cr8O8cdd5xVuAicf5PLePgavzBhd47k31BnKJafoG7QFujv0CxISE5QWp6vQWdAJSDOP2QLnSZjBzRp0kRf8YfITxhNhUzXHR1RdTnEL5+fpHKeixcvtgoD3dauXdsqFSpUsMKUsXBZzwcffGCVrVu36t+KJmMh9hwGQLE8Cz0Ake+h5tAOSEhMLs7zaehi6DxoJpQIth6/g+LhxCyzhsKKrW75PshJ6DzpRH/55Rd9xVsi7zzJMmgC9A3kJ7t371YbNmywnCcD3LL70bBhQ3XYYYdZ5bzzzlNTp8Ldo+R7qoXpEL+UTNsbP4nAz9I4T34hO0FbISExuTjPzdA1EGkMjYQMe6GXIDrX+VAsHE5hfno3H2rcgsvNJgzg7MdMfF44z1yh0+PC3Y4dO6rbb4dB7NiRMMTYrl27rNe++uorq4XIUr9+fctwWW644QY1duxYK/VB3TPq6t8S4tkNsbVyBXQOVAOaBxlinSdhWl924YXE5OI8mWeeDyfCz4Sz4vH0gj6BYlkDHQGdCbHH5xbDhg2zxvS3bdumr3iHOM80MHBE7DpGUy677DLVuXNnVbFixaJrAwcOtCZpJkyYoH87MV37otv+kextz4QvoNugWF6GzoXYqukP3QQJycnFeXJ1CtMm14QGQolI5Dxj4VDZMMgtuKSOwUUWLVqkr3iDOM8UJEq6ZUq1atX0T9nHcp5zxHlmwvtQbygejr/Rad4BLYaE5Cz8WjvPN+07T066ctySXAWxqx5POuc5DhoBucno0aOt98ien1fkvfPk05itRaYOMI6Ri8HZquQuGvLss89aUbH5GsdYGNhj7dq11mvZIM5T8JKF78J59oHzhOzC4RCz2uEG6G9QPHyIxY95GnZBQyAvVkRwGzCj+HtF3jnPN998U3Xq1MlyhH/605/UtGnTPH1akd59e6vyc8qrUXHibigu44gV3PkhYgsg9vdE+aFToVg7MIq1F4rbG2N/b+CSgargxYKsHNgkiGsz+bscu2Qr1Ey8/gL1g3iNK1o4yWfYAF0JcbLPq9Utd999txXY+rvvDp35d4NIO08m12Iahb/85S9W+lSmTmDkcEb08ZMufbuo6nMSb8+k0cXKLBWJVaoukhBdONMdawcUH7ix9kJxnDKWVbNWqYJu9lueXBLGGfMPoDDAMIZsFHmVyTNyzpOzbmy+c5KH4yBMoxC0/dfSbRe8xG63nZM7z0Bhg999plBhKmSukHGbyDhPBlHljBszFgYdy3m+L85T8IZMnCc3k9wNvQ2FmZdfftlqfXoRQSrUznP69OlW1Ol69eqFaiti1x5wnq3EeQresHAOnGcXOM9dxZ0nYz9wzSydZlR2aHHBPJ0n48m6TeicJ2MTclcOK4gBLsJIqu2ZguA0Zp3n2zMLW5XccXcLFLUlXlwwf84551jv9aijjlLt2rXLqAW6CuIkLDcDcMMFVxVsg9IRGuc5ePBgK+gFHU/YEecZXjjjzLWP1PRPpqv2vdsXK9f2vlZd3fvqQ67bKt1RdNxUJwqX3hWULlCNJzZWBV0LVJP2TVTH9h0T/qyXhRO6TsCMBMxYUKNGDctxxhYuK8yEoRCjdJHPoEg4z+uvv94Koxalvd7iPKML9+O/AwWJ77//3nIk7896X1+JFgyQwxi0DKIT7zz/8Y+DgdBTwehc0yDCvfyJAp3EE1jned1111ndcwbSiBriPKMLI0DFrncMArlszwwbXJrI98q0I3a4D2oD3QpxPz735qcjcM6TEYX45sOQbyVbxHlGE66x/DMUtJZnPjlPM2Fk13+w5ckIUYTbSTNZ2B8Y58k3y5Ymxy6ijjjPaPIhhM6i76EP4xHnmR7mOXsFIowk1QdKRyCc57Qfp6naNWqrKa9MCVyGPDcQ5xlNuPOLzrMKFCTEeaaGs+2XQX+FGHybGXYZcCYdvjrP119/XdWoVkNNHztd/ReqAy2Eoo44z+jBTK0tIDrPulCQEOfpDr45z1tuucVaehT/Jrl/lwbIoAJMsRBFxHlGDzpPBgsW5+kvkXaeTGfLN5du8/4/IRoiVRlicII9UBQQ5xk96DyZSrc01AQKEuI83cFT58l8y1z1b4cxkHGiFCOIs3XqdDIpLxHnGV2YFZIpdoOEOE938MR5MhVuyZIl1cSJE/UV+zA0m3GgjGvImc2wIs4zusg6T3+JlPNctWqV9Wac3ofObXJMZ5pNdGy/EecZXcR5+ktknOdnn31mBSEeN26cvuI8zLTITIr3QGuhMCDOM7qI8/SXSDjPZcuWWW+Cy5G84kuIaQGWQ0FGnGdwGQ6Vg/hQNsyFqkNMNWHEpGcPQ1wjGIs4T3+JhPMsXbq06t69uz7zFjrPv0DdoGQpKzh7/zy0DkoEUxAw4b8biPMMLkxhwZw93GEyHuIYe3zqYwPt4wxoEWQQ5+kvoXee3bp1U2XKlNFn/sAgr89pdYRMXheOlTIpFZ3qV1A9KLb1sBJiy4IwsdVGyGnEeUYXcZ7+Emrn+fTTT1uO0+8QcqMhbvBnSlS2HpKlRu0LfQ4ZmNj/VYjwS9AWchpxntGBPZfY9cfiPP0ltM6TqT8ZkNSLG0/HWKg/1BpiKzQR/4bYuow1fsZjNAECvoUYVdppxHkGF67R5N7miyDuc06n0yD2VgziPP0llM7zo48+UlWqVFHPPfecvuIvT0FseTJOHx1iPGwxcLzqByiWWOfJ7rzpwjuJOM9gcwBK1lOJh72W2KjjQXSeCxYssBwKc35FnVA6z8mTJ6vDDz9crVx58CnsJ6bbzpnS+OCm+yG2KOPzW5O7IAZFJWy1snXqNJ26dFInVT9JnwlRIojOM58InfPcuXOndcNPPfWUvuIvdIoXQ4xywz3HTHbFmXfCGdILILNbiYpfbsKZds62chto7JIVx7gVhTU/wDoTIoQ4T38JnfM899xzVYsWLfRZdGA0aS5TYevVETi0OkqpXvV7qdlnz1bW5qihKPv5ohAFxHn6S6ic5zfffKNOOeWUjBMthZFdELeBcgIqp6VLHD5doVTfm/qqOVXnFF77H0rvwkMhvMyCGMSGaTiGQII/hMp5MrQcb3bzZncWlAeNORCdaLIZ/KRsRdGBoPp2iXGehC3S9JlOhYDDgDUcBgpaPM98IjTOc9euXapv377qtNNOU9u25d+3n5NSj0B26ds1znkKoYdj67UgcZ7+EhrnyRvkjb788sv6Sn7yHnQ3xK5bJojzjCYvQnSebIEK/hAa57l8+XLrRnnDglJbIE4wdYaYgS8Z4jyjicmeORES/CE0zrNz586qWbNmat26xME18hkGi2AC/UTJ88V5RpNPoVKQY6szBNuEwnnu27dP1a1bV7Vu3VpfERLBHN5MzfA4xJ0rpE/XPtk7z/dQ2ND/2ToTAgY/a1mq5B+hcJ6DBg1SpUqV0mdCJkyF/gaddeNZ6tMan6rtELf2ZaUVKENRum9Te17ZYzlmVxb05zO7UDgPaqMM2DNATf8FzjPBa0UlGnkMA0konOeQIUOsmJ179+7VV4IB99j369cvkOWWfreoQf0GqUZnNFKDyg1Se/vtzb7chjIYZdBe9WvDX61Pck7fOQn/XSlZls9Q9torTX5tov6y/y8JXysqr6Mk+vcCVHr37m05oUzKeeedd8jv33PPPVbv1GvEeUacnAODsNveH+UmlO9QCkcDhAAQpR1GBw6gPxNXgk4onOeAAQOsjJiCfXJyntv1f4VAwiVr0yDBH0LhPMnvfvc79ec//1mfCZkiIemiCXefoSNbLLi24C2hcZ7169dXV1xxhT4TMkWcZzThEiU6z+aQ4A+hcZ6tWrWySj5uzcwFcZ7R5GWIzrMOJPhDaJznihUrrBt98cUX9RUhE8R5Rg/Z2x4MQuU8OWn07LPPhmImLiiI84wedJ7HQXSe1SDBH0LjPMmoUaOsm2WEJSEzxHlGF6ZxeQcS/CFUzpM0b95cNW3aVJ8J6RDnGV0kkry/hM55jhw5UtWqVUvNn59ZxsF8R5xndBHn6S+hc54//vijdcPjx4/XV4RUiPOMLuI8/SV0zpNMmzbNuumgpB4OMuI8o4s4T38JpfNk+uE//OEP6sILL9RXhGSI84wu4jz9JZTO08AbZ0QVITniPKOLOE9/CbXzZEg43vzSpUv1FSEecZ7RRZynv4TaeRIGSi5btqzasWOHviLEIs4zuojz9JfQO08ybNgwVaVKFZlASoA4z+giztNfIuE8yX333ad+85vfSMDkOMR5Rhdxnv4SGedJOHlUrVo1tWzZMn1FEOcZXcR5+kuknCd599131XHHHacmTZqkr+Q3EydOVIMHD9ZnQpQQ5+kvkXOeZNOmTerss89WXbp00VcEIXqI8/SXSDpPA8dBjzzySLVu3Tp9RRCCA/PrV4F2WXmHC2Hu/XpQ5xh1h8ZCm6BYxHn6S6SdJ1m8eLGVeVO68ULQ2AxdCd0KMc8+43P2ghLxC9QEonM1iPP0l8g7T8JAymXKlFF33nmnviII4Uecp7/khfM0zJgxQ9WpU0f97W9/01cEwX+WQ19qfQ8lYie0BmIUeYM4T3/JK+dpWL16tRUT9MYbb9RXBMF7boe6QV9DhvnQU1Ar6FKIx2uhiRC79RsggzhPf8lL52mgE2VLtFevxONMguA2z0E3Qe9BydgDPQb9P+gHyCDO01/y2nka1qxZo+rWrStOVAgV4jz9RZxnDHSi9evXVz169NBXBCG4iPP0F3GeCdiwYYNq166dqlixolVBQiEce7sZ+gQS/Eecp7+I80zD1KlTre2eTz31lNUyzVc423s9tBUSgoE4T38R55khnFy69dZbVe3atdXs2bP11fzhbmgadAASgoE4T38R55kFCxYsUC1btlSVK1dWp556qlqyZIl+JVr8DHHpzGioJ/QTJAQHcZ7+Is7TAR588EFVqlQpdcopp6iHHnrIGjONAs9DXFtIHQMthYTgIM7TX8R5OgxboXSgrNQGDRqoe++918o1v3v3bv0T4YHddDrOEtDTkBAsxHn6izhPl1m+fLkaM2aMFZSYFV2uXDnVtm3bwHf110OHQ3SeF0NC8BDn6S/iPH3imWeeUS1atLAqv0aNGpZzZfnwww/1TxzkiSeeUM2bN7d+llHh+/fvr7Zs2aJfdQduA6TzvBriDhcheIjz9BdxngGDofP69OljlZIlS1ofTnw54ogjrKVTbsI1nQ2heZAQTMR5+os4zwDDsVJuGT322GMPcaBXXXWV6tixo1Xq1atX7DVuNX3kkUeKyuTJk/VfzJyW0D8gIbiI8/QXcZ4hYOfOner1119XV155pRo+fLjatm2bOnAg9XpL/owp8+fPV3/605+KSvny5Ys52w4dOqjx48cXlcvnXq7wk/ovCUHlDmgGJPiDOE/BSte8di066rpM2D5BNe3XVDVu3Fg1bNjQWobFoQJT2Jp94403igodtOAd46BaUBnoLEjwB3Gegm24TXXRokVF5YYbblA1a9YsKtw8wKEGFp5zR9bcuXOLipAb3OVVG0K/QdWFBH8Q5+kDnIT5PcR1lJyUYTzH7VBU+eyzz4o5z9NPP73IubKcdNJJxZzvsGHDihwzl3oJxWE0+RMgcZ7+Is7TB3ZAXAJEVkL8ErwM+cVGiGOc/4H+DDEtBLM2roD8YNmyZUVDAv/6179UiRIlioYMmA2VzpdDCqawZRs77JAPMPo87aYOJPiDOE8fYISiKyA6J4Z36wCthvyAeXOY/vYLiHBNZ3toPBQWZs6cWWzC68wzz7SMmoWZU1u1alVU2rdvrzZu3FhsQi2MfATReTJ9seAP4jx9gC3PThB5FEJn1QrA4QevQc0hkxsHnWVrPI3/jSpPPvlk0TKuhx9+2MqsapwtNyyYJWAsDzzwgNq/f39RSbfKwSvoPA+DJLaqf4jz9AHTbd8FkSehsZBf9INmQWx19oAGQUxAxvvMdzjmOnDgwKLSvXv3IkdrCneGmY0NbAXb5auvvlKDBg2yWs124OfEcXPBHxjrl5//iBEj9BX3EOepYbf9SogwsRe7Xy9BfoO2lT4SsmXmazPVTV1vKiotm7Us5mirHFtFPXz/w0WlasWqxV5nWbVqlf5rqRkMvQMJ3nPppZce8rl9/fXBLKhOI85Tsw1iRPZ10C+QV2yCekFsXSZTfYgR42OvibIX05YwxbDRLVDnXZ1VmzVtVMED+NKNQhmN8ijK0YVfQhYGj2k7F2Vd8tJhRwd1xeYrEr5mu9yMwn9TSspywQUXFHOYsYVL9NxCnGfA4fpBzrLvhQRvYMjC0047zfryMZYBv6Cy6SD4jBw50tpAws/t8MMPV23atLEmIt1CnGcIqA5dBgmCEBzEeYaAJlB56H1IEIRgIM4zBDSFCqD3IEEQgoE4zxBwDkTnWRqSNMPu8wj0IyQIqRDnGQKM8ywJcRmV4C7XQZKVVEiHOM8QcAZE50ldCgnuMRvi1lyz20wQkiHOMySMgCZAgnswrsH9ECPBc+2nIKRCnGdIeBN6AIpymDy/YUCWBlB3iK38SZAgJEOcZ4jgWJxfIemizj6Iu7jMRBHjGjA6vCAkQ5xniPg79DYkuAOdJx0m4wlcBbWAZOJISIY4zxDBCEvce+8ku6E3ILvwdz6GBCFfEefpEuz+BT18HOOV3giRv0KZsAxiq4xcC5nfF4R8Q5ynCzAmaDeIEcXXQLEwwMdS6Fso0eQPc+EsgeikeJwMRrlfCK2HyM9Qqp9PRBeIf4PcC/WG7LAK4vsUhHxEnKdL/AOaCcVCx9kM4g4W5kmKXQ5Dh8tgzKYFOAB6F0rE/0EvQIQ5jrj2k2N17NbHwi7+c3H6FDLQ8XGGmXB5Dv9NO1wCmfsQhHxDnKdLMCjuFCgRr0OMCn8HFMs/IbODqC80B4qHs8BHQKbFSbiEiX8zHo5LmsX1RjdAhljnycXhdpznUIiOnrPUgpCPiPN0CTrP+ImYtRB3rxCm2OgPxZKJ86SzOxNi154wXw6dIlMn24UJ79hCJo0hriXNBObquRUShHxGnKdLMI8N83hzHNE4NkarZ4uNDovb/xhqjuOiTAFCsRvcBloA0ZnFt0wN3GnEVuIQaDREJ300ZDdtCGfauaOGjp5J78yYKe+PDjlREBJGduK/ZVqyvF9ByEfEeQqCIGSBOE9BEIQsEOcpCIKQBeI8BUEQskCcpyAIQhaI8xQEQbCNUv8f5RbfINbkPqAAAAAASUVORK5CYII=" alt="">
试计算图中
A、
B、
C、D和E点的坐标。
发布时间:2025-02-22 23:40:00