已知正方形ABCD所在平面与正方形ABEF所在平面互相垂直，M为AC上一点，N为BF上一点，且AM=FN=x有，设AB=a（1）求证：MN∥平面CBE；（2）求证：MN⊥AB；（3）当x为何值时，MN取最小值？并求出这个最小值．
已知正方形ABCD所在平面与正方形ABEF所在平面互相垂直，M为AC上一点，N为BF上一点，且AM=FN=x有，设AB=a（1）求证：MN∥平面CBE；（2）求证：MN⊥AB；（3）当x为何值时，MN取最小值？并求出这个最小值．
发布时间：2025-07-02 15:51:33
=
=
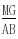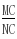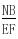∴MG
NH∴MNHG为平行四边形；∴MN∥GH又∵GH⊆面BEC，MN≠⊂面BEC∴MN∥面BEC（2）∵AB⊥BC，AB⊥BE∴AB⊥面BEC∵GH⊆面GEC∴AB⊥GH∵MN∥GH∴MN⊥AB（3）∵面ABCD⊥面ABEF∴BE⊥面ABCD∴BE⊥BC∵BG=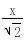
，BH=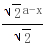
∴MN=GH=
=
=
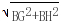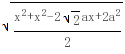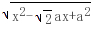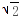（0＜a＜
a）=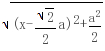
≤
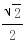a当且仅当x=
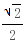a时，等号成立；∴当x=
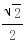a时，MN取最小值
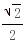a．
