如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
发布时间:2025-03-16 19:00:43
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
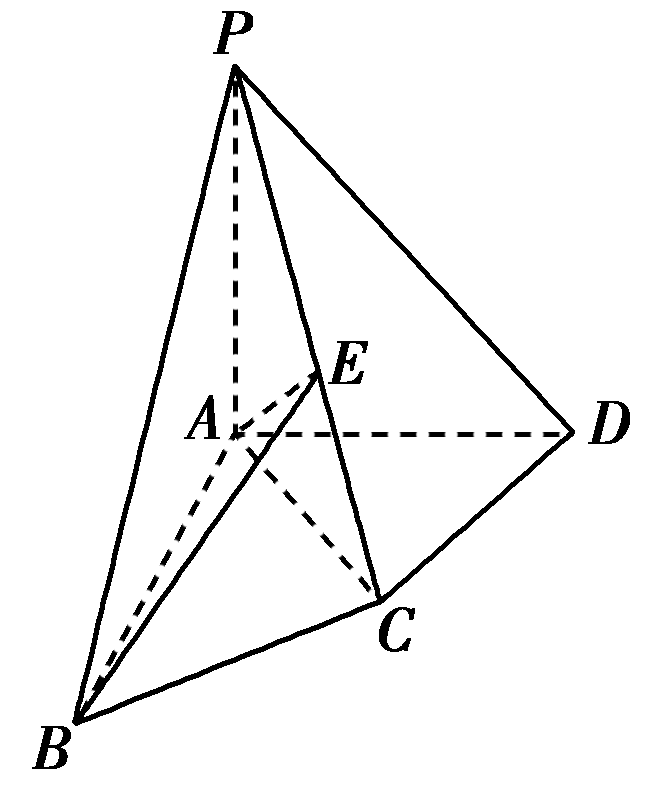 证明: (1)在四棱锥P-ABCD中,∵PA⊥底面ABCD,CD⊂平面ABCD.∴PA⊥CD.∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC.而AE⊂平面PAC,∴CD⊥AE.(2)由PA=AB=BC,∠ABC=60°,可得AC=PA.∵E是PC的中点,∴AE⊥PC.由(1),知AE⊥CD,且PC∩CD=C,∴AE⊥平面PCD.而PD⊂平面PCD,∴AE⊥PD.∵PA⊥底面ABCD,∴PA⊥AB.又∵AB⊥AD且PA∩AD=A,∴AB⊥平面PAD.而PD⊂平面PAD,∴AB⊥PD,又∵AB∩AE=A,∴PD⊥平面ABE.
证明: (1)在四棱锥P-ABCD中,∵PA⊥底面ABCD,CD⊂平面ABCD.∴PA⊥CD.∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC.而AE⊂平面PAC,∴CD⊥AE.(2)由PA=AB=BC,∠ABC=60°,可得AC=PA.∵E是PC的中点,∴AE⊥PC.由(1),知AE⊥CD,且PC∩CD=C,∴AE⊥平面PCD.而PD⊂平面PCD,∴AE⊥PD.∵PA⊥底面ABCD,∴PA⊥AB.又∵AB⊥AD且PA∩AD=A,∴AB⊥平面PAD.而PD⊂平面PAD,∴AB⊥PD,又∵AB∩AE=A,∴PD⊥平面ABE.
