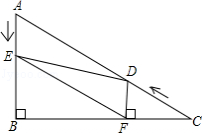
（2011•河南）如图，在Rt△ABC中，∠B=90°，BC=5https://bgk-photo.cdn.bcebos.com/e61190ef76c6a7ef945fbf46edfaaf51f3de6650.jpg，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．（1）求证：AE=DF；（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．（3）当t为何值时，△DEF为直角三角形？请说明理由．https://bgk-photo.cdn.bcebos.com/f2deb48f8c5494ee925b18793df5e0fe99257e50.jpg
（2011•河南）如图，在Rt△ABC中，∠B=90°，BC=5https://bgk-photo.cdn.bcebos.com/e61190ef76c6a7ef945fbf46edfaaf51f3de6650.jpg，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点
D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接D
E、E
F、（1）求证：AE=DF；（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．（3）当t为何值时，△DEF为直角三角形？请说明理由．https://bgk-photo.cdn.bcebos.com/f2deb48f8c5494ee925b18793df5e0fe99257e50.jpg
发布时间：2025-03-30 12:25:53
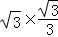=5，∴AC=2AB=10．∴AD=AC﹣DC=10﹣2t．若使▱AEFD为菱形，则需AE=AD，即t=10﹣2t，t=
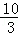．即当t=
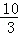时，四边形AEFD为菱形．（3）解：①∠EDF=90°时，四边形EBFD为矩形．在Rt△AED中，∠ADE=∠C=30°，∴AD=2AE．即10﹣2t=2t，t=
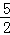．②∠DEF=90°时，由（2）四边形AEFD为平行四边形知EF∥AD，∴∠ADE=∠DEF=90°．∵∠A=90°﹣∠C=60°，∴AD=AE•cos60°．即10﹣2t=
t，t=4．③∠EFD=90°时，此种情况不存在．综上所述，当t=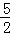
或4时，△DEF为直角三角形．
