如图,在正方形ABCD中,E是边AB上的任意一点(不与点A,B重合),连接DE,作点A关于直线DE的对称点为F,连接EF并延长交BC于点G.(1)依题意补全图形,连接DG,求∠EDG的度数;(2)过点E作EH⊥DE交DG的延长线于点H,连接BH.线段BH与AE有怎样的数量关系,请写出结论并证明.https://bgk-photo.cdn.bcebos.com/10dfa9ec8a13632703434d52818fa0ec08fac721.jpg
如图,在正方形ABCD中,E是边AB上的任意一点(不与点A,B重合),连接DE,作点A关于直线DE的对称点为F,连接EF并延长交BC于点G.(1)依题意补全图形,连接DG,求∠EDG的度数;(2)过点E作EH⊥DE交DG的延长线于点H,连接BH.线段BH与AE有怎样的数量关系,请写出结论并证明.https://bgk-photo.cdn.bcebos.com/10dfa9ec8a13632703434d52818fa0ec08fac721.jpg
发布时间:2025-03-21 22:57:40
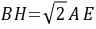 ,证明见解析.[分析](1)根据题目的已知,作图即可;连接
,证明见解析.[分析](1)根据题目的已知,作图即可;连接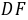 ,根据对称得:
,根据对称得: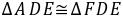 ,再由
,再由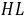 证明
证明 ,可得结论;(2)过点H作
,可得结论;(2)过点H作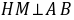 的延长线于点M,根据
的延长线于点M,根据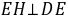 得到
得到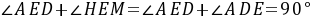 ,
,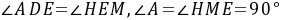 由(1)得:
由(1)得: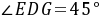 ,则
,则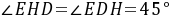 ,可证
,可证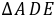 ≌
≌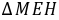 ,则有
,则有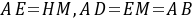 ,可得
,可得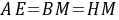 ,即
,即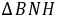 是等腰直角三角形,可证得
是等腰直角三角形,可证得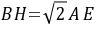 .[详解](1)补全的图形,如图所示.
.[详解](1)补全的图形,如图所示.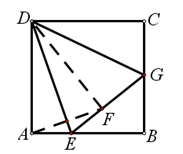 连接DF∵四边形ABCD是正方形,∴
连接DF∵四边形ABCD是正方形,∴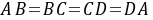 ,
,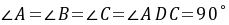 ∵点
∵点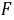 为点
为点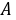 关于
关于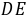 的对称点,∴
的对称点,∴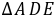 ≌
≌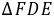 .∴
.∴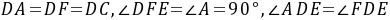 ,∴
,∴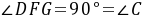 .又∵
.又∵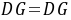 ,∴
,∴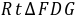 ≌
≌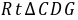 (HL)∴
(HL)∴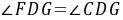 ,∴
,∴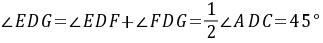 .(2)如图所示.线段BH与AE的数量关系为
.(2)如图所示.线段BH与AE的数量关系为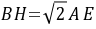 如图,过点H作
如图,过点H作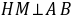 的延长线于点M,
的延长线于点M,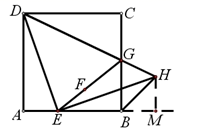
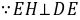 ,∴
,∴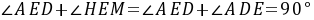 ,∴
,∴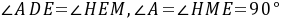 由(1)得:
由(1)得: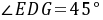 ∴
∴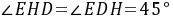 ∴
∴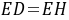 ∴
∴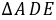 ≌
≌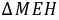 ∴
∴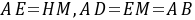
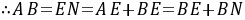 ,∴
,∴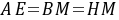
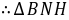 是等腰直角三角形,∴
是等腰直角三角形,∴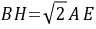 .[点睛]本题考查了正方形的性质,全等三角形的判定定理和性质定理,对称的性质,等腰直角三角形的性质等知识,解决本题的关键是利用正方形的性质得到相等的边和相等的角,证明三角形全等,作出辅助线也是解决本题的关键.
.[点睛]本题考查了正方形的性质,全等三角形的判定定理和性质定理,对称的性质,等腰直角三角形的性质等知识,解决本题的关键是利用正方形的性质得到相等的边和相等的角,证明三角形全等,作出辅助线也是解决本题的关键.

