请在下方输入要搜索的题目：

已知函数f（x）=xlnx ax（a∈R）（I）若函数f（x）在区间[e2， ∞）上为增函数，求a的取值范围；（II）若对任意x∈（1， ∞），f（x）＞k（x-1） ax-x恒成立，求正整数k的值．

发布时间：2025-05-13 11:35:08

推荐参考答案 ( 由快搜搜题库官方老师解答 )

联系客服

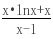答案：（Ⅰ）由f（x）=xlnx ax，得：f′（x）=lnx a 1∵函数f（x）在区间[e2， ∞）上为增函数，∴当x∈[e2， ∞）时f′（x）≥0，即lnx a 1≥0在区间[e2， ∞）上恒成立，∴a≥-1-lnx．又当x∈[e2， ∞）时，lnx∈[2， ∞），∴-1-lnx∈（-∞，-3]．∴a≥-3；（Ⅱ）若对任意x∈（1， ∞），f（x）＞k（x-1） ax-x恒成立，即x•lnx ax＞k（x-1） ax-x恒成立，也就是k（x-1）＜x•lnx ax-ax x恒成立，∵x∈（1， ∞），∴x-1＞0．则问题转化为k＜

对任意x∈（1， ∞）恒成立，设函数h（x）=

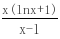，则h′(x)=

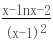，再设m（x）=x-lnx-2，则m′(x)=1-

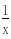．∵x∈（1， ∞），∴m′（x）＞0，则m（x）=x-lnx-2在（1， ∞）上为增函数，∵m（1）=1-ln1-2=-1，m（2）=2-ln2-2=-ln2，m（3）=3-ln3-2=1-ln3＜0，m（4）=4-ln4-2=2-ln4＞0．∴∃x0∈（3，4），使m（x0）=x0-lnx0-2=0．∴当x∈（1，x0）时，m（x）＜0，h′（x）＜0，∴h(x)=

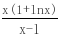在（1，x0）上递减，x∈（x0， ∞）时，m（x）＞0，h′（x）＞0，∴h(x)=

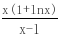在（x0， ∞）上递增，∴h（x）的最小值为h（x0）=

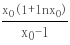．∵m（x0）=x0-lnx0-2=0，∴lnx0 1=x0-1，代入函数h（x）=

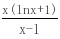得h（x0）=x0，∵x0∈（3，4），且k＜h（x）对任意x∈（1， ∞）恒成立，∴k＜h（x）min=x0，∴k≤3，∴k的值为1，2，3．