https://bgk-photo.cdn.bcebos.com/doc/pic/item/d6ca7bcb0a46f21f54ec3894f1246b600d33ae19.jpg如图，两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起，∠DEA=∠ACB=90°，∠DAE=∠ABC=30°，E、A、C三点在一条直线上，连接BD，取BD中点M，连接ME、MC，试判断△EMC的形状，并说明理由．
https://bgk-photo.cdn.bcebos.com/doc/pic/item/d6ca7bcb0a46f21f54ec3894f1246b600d33ae19.jpg如图，两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起，∠DEA=∠ACB=90°，∠DAE=∠ABC=30°，
E、
A、C三点在一条直线上，连接BD，取BD中点M，连接M
E、MC，试判断△EMC的形状，并说明理由．
发布时间：2025-07-13 11:33:17
解：△EMC的形状是等腰直角三角形，理由是：连接AM，∵∠8=30°，∠9=60°，∴∠DAB=180°-30°-60°=90°，∵M为BD中点，AD=AB（已知两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起），∴AM⊥BD（等腰三角形底边的高也平分底边）AM=BM=DM（直角三角形斜边上中线等于斜边的一半）∴∠5=∠6=
（180°-90°）=45°，∠4=∠BDA=45°，∵∠7=30°，∴∠MBC=45° 30°=75°，同理∠MAE=75°=∠MBC，在△BCM和△AEM中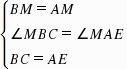
，∴△BCM≌△AEM（SAS），∴EM=CM，∠3=∠2，∵AM⊥BD，∴∠1 ∠2=90°，∴∠1 ∠3=90°，∴△EMC是等腰直角三角形．
