如图,在等腰直角三角形ABC中,AC=BC,D是边BC的中点,E是边AB上的点,且AE=2BE,求证:AD⊥CE.
如图,在等腰直角三角形ABC中,AC=BC,D是边BC的中点,E是边AB上的点,且AE=2BE,求证:AD⊥C
E、
发布时间:2025-02-28 11:38:59
如图,在等腰直角三角形ABC中,AC=BC,D是边BC的中点,E是边AB上的点,且AE=2BE,求证:AD⊥C
E、
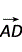 ·
·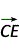 =
=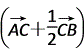 ·
·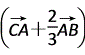 =
=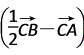 ·
·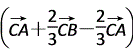 =
=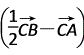 ·
·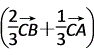 =
=
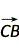 2-
2-
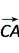 ·
·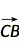 -
-
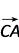 2.∵BC⊥CA,∴
2.∵BC⊥CA,∴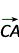 ·
·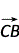 =0.又BC=CA,∴|
=0.又BC=CA,∴|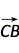 |=|
|=|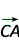 |,∴
|,∴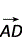 ·
·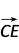 =
= (|
(|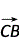 |2-|
|2-|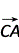 |2)=0,∴
|2)=0,∴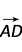 ⊥
⊥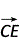 ,即AD⊥CE.
,即AD⊥CE.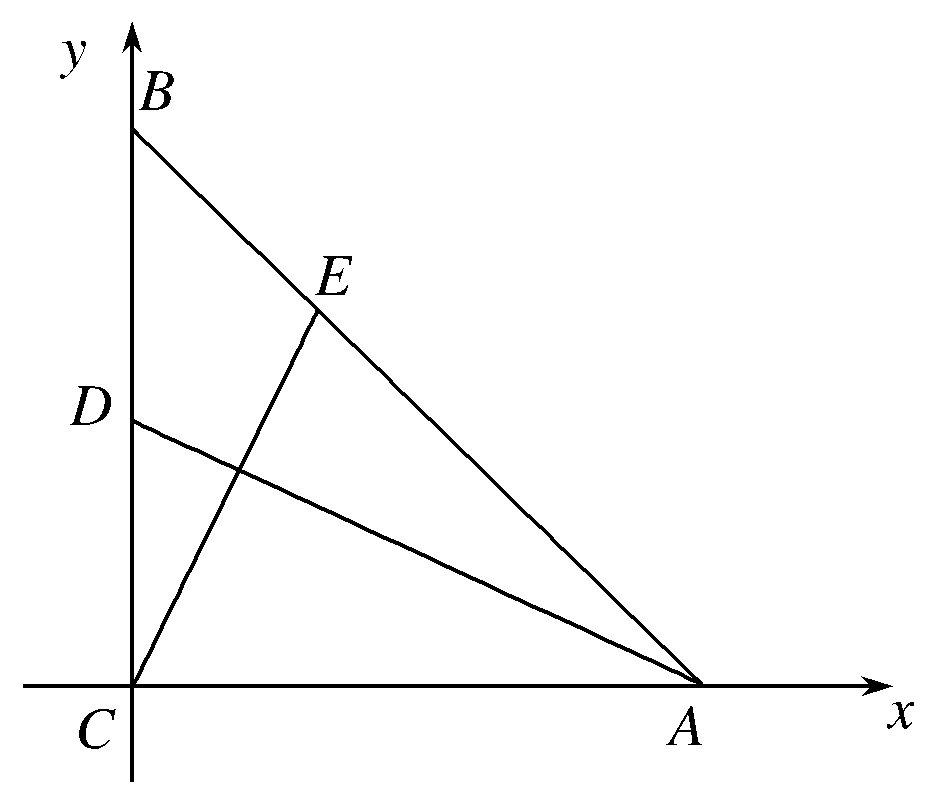 解法二(坐标法)以CA,CB所在直线为坐标轴,建立如下图的平面直角坐标系,设 |
解法二(坐标法)以CA,CB所在直线为坐标轴,建立如下图的平面直角坐标系,设 |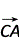 |=|
|=|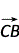 |=a,∴C(0,0),A(a,0),B(0,a),E
|=a,∴C(0,0),A(a,0),B(0,a),E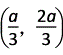 ,D
,D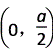 ,∴
,∴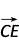 =
=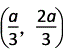 ,
,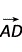 =
=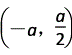 ,∴
,∴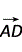 ·
·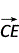 =-
=-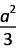
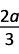 ×
×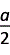 =-
=-
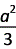 =0,∴
=0,∴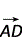 ⊥
⊥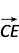 ,即AD⊥CE.
,即AD⊥CE.