已知点P是椭圆+=1上的动点,且与椭圆的四个顶点不重合,F1、F2分别是椭圆的左、右焦点,O为坐标原点,若点M是∠F1PF2的角平分线上的一点,且F1M⊥MP,则 |OM|的取值范围是________.
已知点P是椭圆+=1上的动点,且与椭圆的四个顶点不重合,F1、F2分别是椭圆的左、右焦点,O为坐标原点,若点M是∠F1PF2的角平分线上的一点,且F1M⊥MP,则 |OM|的取值范围是________.
发布时间:2024-11-16 15:02:01
已知点P是椭圆+=1上的动点,且与椭圆的四个顶点不重合,F1、F2分别是椭圆的左、右焦点,O为坐标原点,若点M是∠F1PF2的角平分线上的一点,且F1M⊥MP,则 |OM|的取值范围是________.
 解析 解法一:如图,延长PF2,F1M,交于点N,∵PM是∠F1PF2的角平分线,且F1M⊥MP,∴|PN|=|PF1|,M为F1N的中点,∵O为F1F2的中点,M为F1N的中点,∴|OM|=|F2N|=||PN|-|PF2||=||PF1|-|PF2||,对于椭圆+=1(a>b>0,xy≠0),设点P的坐标为(x0,y0)(-a
解析 解法一:如图,延长PF2,F1M,交于点N,∵PM是∠F1PF2的角平分线,且F1M⊥MP,∴|PN|=|PF1|,M为F1N的中点,∵O为F1F2的中点,M为F1N的中点,∴|OM|=|F2N|=||PN|-|PF2||=||PF1|-|PF2||,对于椭圆+=1(a>b>0,xy≠0),设点P的坐标为(x0,y0)(-a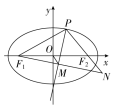 解法三:如图,延长PF2,F1M交于点N,∵PM是∠F1PF2的角平分线,且F1M⊥MP,∴|PN|=|PF1|,M为F1N的中点,又O为F1F2的中点,∴|OM|=|F2N|=||PN|-|PF2||=||PF1|-|PF2||,又 |PF1|+|PF2|=10,∴|OM|=|2|PF1|-10|=||PF1|-5|,又 |PF1|∈(1,5)∪(5,9),∴|OM|∈(0,4),故 |OM|的取值范围是(0,4).
解法三:如图,延长PF2,F1M交于点N,∵PM是∠F1PF2的角平分线,且F1M⊥MP,∴|PN|=|PF1|,M为F1N的中点,又O为F1F2的中点,∴|OM|=|F2N|=||PN|-|PF2||=||PF1|-|PF2||,又 |PF1|+|PF2|=10,∴|OM|=|2|PF1|-10|=||PF1|-5|,又 |PF1|∈(1,5)∪(5,9),∴|OM|∈(0,4),故 |OM|的取值范围是(0,4).
