如图，Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片，点O与原点重合，点https://bgk-photo.cdn.bcebos.com/doc/pic/item/91ef76c6a7efce1b612f770da851f3deb58f65f5.jpgA在x轴上，点C在y轴上，OC=https://bgk-photo.cdn.bcebos.com/doc/pic/item/b3119313b07eca80b3278620962397dda04483d3.jpg，∠CAO=30度．将Rt△OAC折叠，使OC边落在AC边上，点O与点D重合，折痕为CE．（1）求折痕CE所在直线的解析式；（2）求点D的坐标；（3）设点M为直线CE上的一点，过点M作AC的平行线，交y轴于点N，是否存在这样的点M，使得以M、N、D、C为顶点的四边形是平行四边形？若存在，请求出符合条件的点M的坐标；若不存在，请说明理由．
如图，Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片，点O与原点重合，点https://bgk-photo.cdn.bcebos.com/doc/pic/item/91ef76c6a7efce1b612f770da851f3deb58f65f5.jpgA在x轴上，点C在y轴上，OC=https://bgk-photo.cdn.bcebos.com/doc/pic/item/b3119313b07eca80b3278620962397dda04483d3.jpg，∠CAO=30度．将Rt△OAC折叠，使OC边落在AC边上，点O与点D重合，折痕为C
E、（1）求折痕CE所在直线的解析式；（2）求点D的坐标；（3）设点M为直线CE上的一点，过点M作AC的平行线，交y轴于点N，是否存在这样的点M，使得以M、N、
D、C为顶点的四边形是平行四边形？若存在，请求出符合条件的点M的坐标；若不存在，请说明理由．
发布时间：2025-03-15 13:58:26
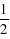∠OCA=30°，∴在Rt△COE中，OE=OC•tan∠OCE=
×
=1，∴点E的坐标是（1，0），设直线CE的解析式为y=kx b．把点C（0，
），E（1，0）代入得
，∴
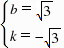，∴直线CE的解析式为y=-
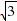x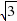 
．（2）在Rt△AOC中，AC=
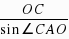=2
，AO=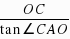
=3，∵CD=OC=
，∴AD=AC-CD=2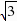
-
=
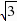，过点D作DF⊥OA于点F，在Rt△AFD中，DF=AD•sin∠CAO=
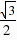，AF=AD•cos∠CAO=
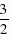，∴OF=AO-AF=
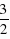．∴点D的坐标是（
，
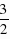）．（3）存在两个符合条件的M点，
第一种情况：此点在第四象限内，设为M1，延长DF交直线CE于M1，连接M1O，M1O∥AC，则有DM1∥y轴，∵OF=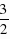
，∴设点M1的坐标为（
，y1），又∵点M1在直线CE上，∴将点M1的坐标代入y=-
x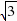 
中，得y1=-
×
=-
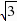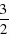
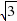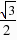，即FM1=
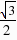．∴点M1的坐标是（
，-
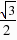），又∵DM1=DF FM1=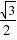
=
，OC=
，∴DM1=OC，又∵DM1∥OC，∴四边形CDM1O为平行四边形，又∵点O在y轴上，∴点M1是符合条件的点．第二种情况：此点在第二象限内，设为M2，过点D作DN∥CE交y轴于N，过N点作NM2∥CD交直线CE于点M2，则四边形M2NDC为平行四边形，∴M2N=CD=
，∵M2N∥CD，DN∥CE，∴∠NM2C=∠ACE，∠OCE=∠M2CN，∴CN=M2N，∵M2N=CD=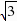
，∴CN=
，作M2H⊥y轴于点H，∵M2N∥CD，∴∠M2NC=∠NCD，∴∠M2NH=∠OCA=60°，在Rt△M2NH中，M2H=M2N•sin60°=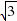
×
=
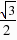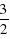，NH=M2N•cos60°=
×
=
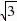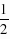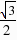，∴HO=HN CN OC=
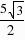，∴M2（-
，
），∴点M2是符合条件的点，综上所述，符合条件的两个点的坐标分别为M1（
，-
），M2（-
，
）．
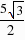