如图,在多面体ABCDEF中,已知四边形ABCD是边长为2的正方形,△BCF为正三角形,G,H分别为BC,EF的中点,EF=4且EF∥AB,EF⊥FB.https://bgk-photo.cdn.bcebos.com/86d6277f9e2f07083225f160f924b899a901f2aa.jpg(1)求证:GH∥平面EAD;(2)求证:FG⊥平面ABCD.
如图,在多面体ABCDEF中,已知四边形ABCD是边长为2的正方形,△BCF为正三角形,G,H分别为BC,EF的中点,EF=4且EF∥AB,EF⊥F
B、https://bgk-photo.cdn.bcebos.com/86d6277f9e2f07083225f160f924b899a901f2aa.jpg(1)求证:GH∥平面EAD;(2)求证:FG⊥平面ABC
D、
发布时间：2025-06-17 19:52:19
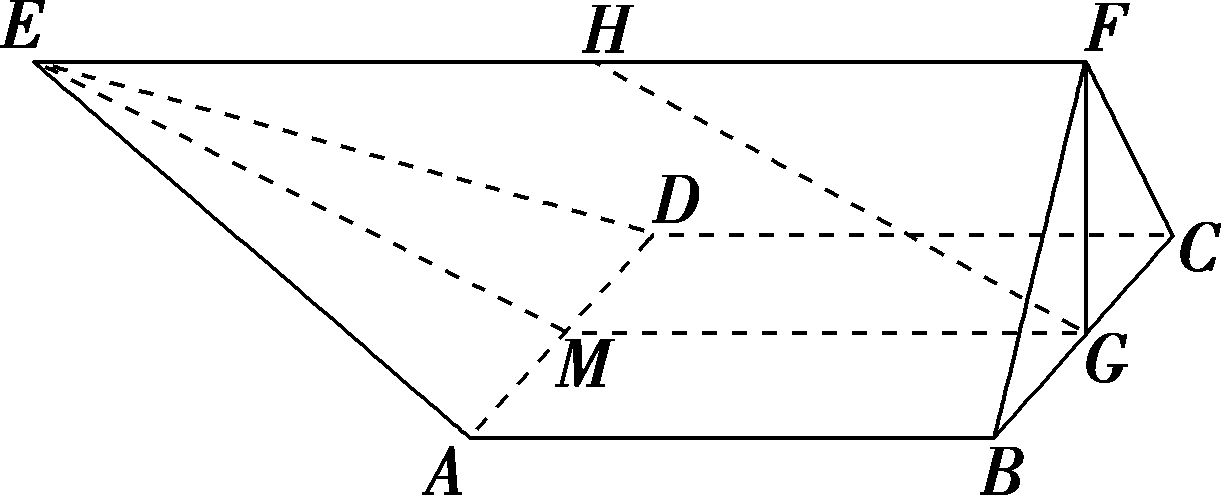因为EF∥AB,M,G分别为AD,BC的中点,所以MG∥EF.因为H为EF的中点,EF=4,AB=2,所以EH=AB=MG,所以四边形EMGH为平行四边形,所以GH∥EM,又因为GH⊄平面EAD,EM⊂平面EAD,所以GH∥平面EAD.(2)因为EF⊥FB,EF∥AB,所以AB⊥FB.在正方形ABCD中,AB⊥BC,所以AB⊥平面FBC.又FG⊂平面FBC,所以AB⊥FG.在正△FBC中,FG⊥BC,所以FG⊥平面ABCD.[B 能力提升]
