已知数列{an}的前n项和为Sn,满足Sn=2an-2(n∈N*),数列{bn}中b1=1,点P(bn,bn 1)在直线x-y 2=0上。(1) 求数列{an}、{bn}的通项公式;(2) 设cn=anbn,求数列{cn}的前n项和Tn,并求满足Tn<167的最大正整数n。
已知数列{an}的前n项和为Sn,满足Sn=2an-2(n∈N*),数列{bn}中b1=1,点P(bn,bn 1)在直线x-y 2=0上。(1) 求数列{an}、{bn}的通项公式;(2) 设cn=anbn,求数列{cn}的前n项和Tn,并求满足Tn<167的最大正整数n。
发布时间:2025-03-30 08:13:03
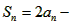 ,Sn-1=2
,Sn-1=2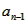 -2(n≥2);两式相减得Sn-Sn-1=an=2an-2an-1(n≥2)∴
-2(n≥2);两式相减得Sn-Sn-1=an=2an-2an-1(n≥2)∴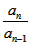 =2(n≥2)又S1=a1=2a1-2即a1=2∴数列{an}是以2为首项2为公比的等比数列,∴an=2n有点(bn,bn 1)在直线x-y 2=0上,∴
=2(n≥2)又S1=a1=2a1-2即a1=2∴数列{an}是以2为首项2为公比的等比数列,∴an=2n有点(bn,bn 1)在直线x-y 2=0上,∴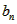 -
-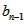 2=0,∴
2=0,∴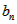 -
- =2即数列{bn}是以1为首项2为公差的等差数列。∴bn=2n-1(2)
=2即数列{bn}是以1为首项2为公差的等差数列。∴bn=2n-1(2)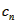 =
=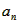
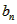 =(2n-1)2n∴Tn=1
=(2n-1)2n∴Tn=1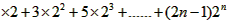 2Tn=1
2Tn=1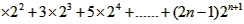 两式相减得- Tn=1
两式相减得- Tn=1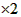 (
(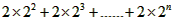 )-(2n-1)2n 1∴Tn=
)-(2n-1)2n 1∴Tn=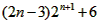 又Tn<167即
又Tn<167即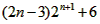 <167易知Tn递增:当n=4时
<167易知Tn递增:当n=4时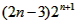 =160当n=5时
=160当n=5时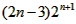 =448故满足条件Tn<167的最大正整数n为4.
=448故满足条件Tn<167的最大正整数n为4.

