如图1，已知∠ABC=90°，△ABE是等边三角形，点P为射线BC上任意一点（点P与点B不重合），连接AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连接QE并延长交射线BC于点F．（1）如图2，当BP=BA时，∠EBF=______°，猜想∠QFC=______°；（2）如图1，当点P为射线BC上任意一点时，猜想∠QFC的度数，并加以证明；（3）已知线段AB=2https://bgk-photo.cdn.bcebos.com/doc/pic/item/b64543a98226cffcc36e9675be014a90f703eab5.jpg，设BP=x，点Q到射线BC的距离为y，求https://bgk-photo.cdn.bcebos.com/doc/pic/item/6159252dd42a283404161fcc5cb5c9ea14cebf40.jpgy关于x的函数关系式．
如图1，已知∠ABC=90°，△ABE是等边三角形，点P为射线BC上任意一点（点P与点B不重合），连接AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连接QE并延长交射线BC于点
F、（1）如图2，当BP=BA时，∠EBF=______°，猜想∠QFC=______°；（2）如图1，当点P为射线BC上任意一点时，猜想∠QFC的度数，并加以证明；（3）已知线段AB=2https://bgk-photo.cdn.bcebos.com/doc/pic/item/b64543a98226cffcc36e9675be014a90f703eab5.jpg，设BP=x，点Q到射线BC的距离为y，求https://bgk-photo.cdn.bcebos.com/doc/pic/item/6159252dd42a283404161fcc5cb5c9ea14cebf40.jpgy关于x的函数关系式．
发布时间：2025-03-07 14:09:53
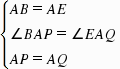，∴△ABP≌△AEQ （SAS） ∴∠AEQ=∠ABP=90° ∴∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°，∴∠QFC=∠EBF ∠BEF=30° 30°=60°；（3）在图1中，过点F作FG⊥BE于点G．
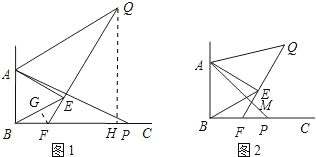∵△ABE是等边三角形，∴BE=AB=2
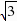．由（1）得∠EBF=30°．又∵∠QFC=60°∴∠EBF=∠BEF，∴BF=EF，∵FG⊥BE∴BG=
=
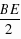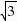，∴BF=
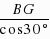=2．∴EF=2． （1分）∵在Rt△ABP和Rt△AEQ中，
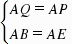∴△ABP≌△AEQ．设QE=BP=x，则QF=QE EF=x 2． （2分）过点Q作QH⊥BC，垂足为H．在Rt△QHF中，y=QH=sin60°×QF=
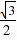（x 2）．（x＞0）即y关于x的函数关系式是：y=
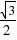x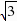 
． （3分）
