如图①，已知点D在AB上，△ABC和△ADE都是等腰直角三角形，∠ABC=∠ADE=90°，且M为EC的中点．（1）求证：△BMD为等腰直角三角形．（思路点拨：考虑M为EC的中点的作用，可以延长DM交BC于N，构造△CMN≌△EMD，于是ED=CN=DA，即可以证明△BND也是等腰直角三角形，且BM是等腰三角形底边的中线就可以了．）请你完成证明过程．（2）将△ADE绕点A再逆时针旋转90°时（如图②所示位置），△BMD为等腰直角三角形的结论是否仍成立？若成立，请证明：若不成立，请说明理由．https://bgk-photo.cdn.bcebos.com/doc/pic/item/5bafa40f4bfbfbedec29a6b87ff0f736aec31f80.jpg
如图①，已知点D在AB上，△ABC和△ADE都是等腰直角三角形，∠ABC=∠ADE=90°，且M为EC的中点．（1）求证：△BMD为等腰直角三角形．（思路点拨：考虑M为EC的中点的作用，可以延长DM交BC于N，构造△CMN≌△EMD，于是ED=CN=DA，即可以证明△BND也是等腰直角三角形，且BM是等腰三角形底边的中线就可以了．）请你完成证明过程．（2）将△ADE绕点A再逆时针旋转90°时（如图②所示位置），△BMD为等腰直角三角形的结论是否仍成立？若成立，请证明：若不成立，请说明理由．https://bgk-photo.cdn.bcebos.com/doc/pic/item/5bafa40f4bfbfbedec29a6b87ff0f736aec31f80.jpg
发布时间：2025-04-04 18:39:57
（1）证明：延长DM交BC于N，∵∠EDA=∠ABC=90°，∴DE∥BC，∴∠DEM=∠MCB，在△EMD和△CMN中
，∴△EMD≌△CMN，∴CN=DE=DA，MN=MD，∵BA=BC，∴BD=BN，∴△DBN是等腰直角三角形，且BM是底边的中线，∴BM⊥DM，∠DBM=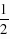
∠DBN=45°=∠BDM，∴△BMD为等腰直角三角形．（2）解：△BMD为等腰直角三角形的结论仍成立，
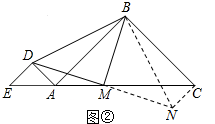证明：作CN∥DE交DM的延长线于N，连接BN，∴∠E=∠MCN=45°，∵∠DME=∠NMC，EM=CM，∴△EMD≌△CMN（ASA），∴CN=DE=DA，MN=MD，又∵∠DAB=180°-∠DAE-∠BAC=90°，∠BCN=∠BCM ∠NCM=45° 45°=90°，∴∠DAB=∠BCN，在△DBA和△NBC中
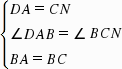，∴△DBA≌△NBC，∴∠DBA=∠NBC，DB=BN，∴∠DBN=∠ABC=90°，∴△DBN是等腰直角三角形，且BM是底边的中线，∴BM⊥DM，∠DBM=
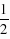∠DBN=45°=∠BDM，∴△BMD为等腰直角三角形．
