https://bgk-photo.cdn.bcebos.com/doc/pic/item/f9dcd100baa1cd110dac78e7be12c8fcc2ce2dda.jpg如图,在平面直角坐标系中,抛物线的顶点A(-1,0)在x轴上,与y轴交于点B,点C(1,4)为抛物线上一点,CD∥x轴交抛物线于点D.(1)求抛物线的解析式;(2)点P为抛物线对称轴左侧图象上一动点,设点P的横坐标为t,△PBC的面积为S,求S与t的函数关系式;(3)在(2)的条件下,作直线AE⊥x轴,交线段CD于点E,连接AP、PE,当∠APE=90°时,求tan∠PCE的值.
https://bgk-photo.cdn.bcebos.com/doc/pic/item/f9dcd100baa1cd110dac78e7be12c8fcc2ce2dda.jpg如图,在平面直角坐标系中,抛物线的顶点A(-1,0)在x轴上,与y轴交于点B,点C(1,4)为抛物线上一点,CD∥x轴交抛物线于点
D、(1)求抛物线的解析式;(2)点P为抛物线对称轴左侧图象上一动点,设点P的横坐标为t,△PBC的面积为S,求S与t的函数关系式;(3)在(2)的条件下,作直线AE⊥x轴,交线段CD于点E,连接AP、PE,当∠APE=90°时,求tan∠PCE的值.
发布时间:2025-02-22 22:52:34
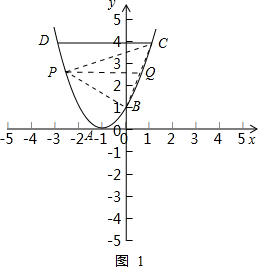 y=x2 2x 1,当x=0,y=1,∴点B(0,1),设直线BC解析式为:y=mx n,把点B(0,1),和点C(1,4)代入得:
y=x2 2x 1,当x=0,y=1,∴点B(0,1),设直线BC解析式为:y=mx n,把点B(0,1),和点C(1,4)代入得: 解得:
解得: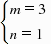 ,∴y=3x 1,设点P的横坐标为t,则纵坐标为:t2 2t 1,把y=t2 2t 1代入y=3x 1,得:x=
,∴y=3x 1,设点P的横坐标为t,则纵坐标为:t2 2t 1,把y=t2 2t 1代入y=3x 1,得:x=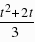 ,∴PQ=
,∴PQ=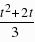 -t=
-t=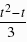 ,∴△PBC的面积为S=S△PCQ S△PQB=
,∴△PBC的面积为S=S△PCQ S△PQB=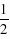 ×PQ×[4-(t2 2t 1) (t2 2t 1)-1]=
×PQ×[4-(t2 2t 1) (t2 2t 1)-1]= ×PQ×(4-1)=
×PQ×(4-1)=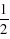 ×
×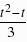 ×3=
×3=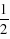 t2-
t2-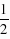 t,∴S=
t,∴S= t2-
t2-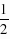 t.(3)如图2,过点P作平行于y轴的直线,交x轴于点M,交CD于点H,
t.(3)如图2,过点P作平行于y轴的直线,交x轴于点M,交CD于点H,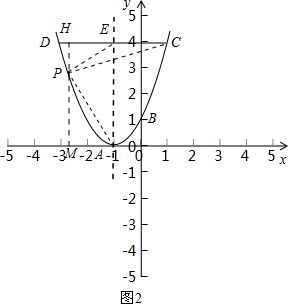 ∵CD∥x轴,∴PH⊥CD,PM⊥x轴,∴∠PHE=∠AMP=90°,∵∠APE=90°,∴∠HPE ∠APM=90°,∵∠HPE ∠PEH=90°,∴∠APM=∠PEH,∴△HPE∽△MAP,∴
∵CD∥x轴,∴PH⊥CD,PM⊥x轴,∴∠PHE=∠AMP=90°,∵∠APE=90°,∴∠HPE ∠APM=90°,∵∠HPE ∠PEH=90°,∴∠APM=∠PEH,∴△HPE∽△MAP,∴ ,由(2)点P(t,t2 2t 1),∴AM=-1-t,PM=t2 2t 1,∵CD∥x轴,点C(1,4),∴PH=4-(t2 2t 1)=3-(t2 2t),HE=AM=-1-t,∴
,由(2)点P(t,t2 2t 1),∴AM=-1-t,PM=t2 2t 1,∵CD∥x轴,点C(1,4),∴PH=4-(t2 2t 1)=3-(t2 2t),HE=AM=-1-t,∴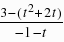 =
=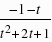 ,解得:t=-1-
,解得:t=-1-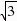 ,或t=-1
,或t=-1 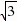 (舍去),∴PH=3-(t2 2t)=1,CH=1-(-1-
(舍去),∴PH=3-(t2 2t)=1,CH=1-(-1-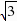 )=2
)=2 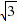 ,在直角三角形PHE中:tan∠PCE=
,在直角三角形PHE中:tan∠PCE=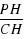 =
=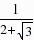 =2-
=2-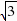 .
.

