如图，在平面直角坐标系中，抛物线y=﹣x2 ax b交x轴于A（1，0），B（3，0）两点，点P是抛物线上在第一象限内的一点，直线BP与y轴相交于点C．实用文档文案大全 （1）求抛物线y=﹣x2 ax b的解析式；（2）当点P是线段BC的中点时，求点P的坐标；（3）在（2）的条件下，求sin∠OCB的值．https://bgk-photo.cdn.bcebos.com/79f0f736afc37931fa534a56fbc4b74543a91192.jpg
如图，在平面直角坐标系中，抛物线y=﹣x2 ax b交x轴于A（1，0），B（3，0）两点，点P是抛物线上在第一象限内的一点，直线BP与y轴相交于点
C、实用文档文案大全 （1）求抛物线y=﹣x2 ax b的解析式；（2）当点P是线段BC的中点时，求点P的坐标；（3）在（2）的条件下，求sin∠OCB的值．https://bgk-photo.cdn.bcebos.com/79f0f736afc37931fa534a56fbc4b74543a91192.jpg
发布时间：2025-02-26 14:14:37
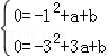，解得，a=4，b=﹣3，∴抛物线的解析式为：y=﹣x2 4x﹣3；（2）∵点C在y轴上，所以C点横坐标x=0，∵点P是线段BC的中点，∴点P横坐标xP
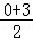==，∵点P在抛物线y=﹣x2 4x﹣3上，∴yP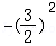
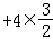=﹣3=，∴点P的坐标为（，）；（3）∵点P的坐标为（，），点P是线段BC的中点，实用文档文案大全 ∴点C的纵坐标为2×﹣0=，∴点C的坐标为（0，），∴
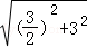BC=
=，∴sin∠
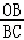OCB=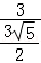
=
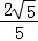=【点评】本题主要考查了待定系数法求二次函数解析式和解直角三角形，利用中点求得点P的坐标是解答此题的关键．
